In This Topic
Null hypothesis and alternative hypothesis
- Null hypothesis
- The null hypothesis states that a population parameter (such as the mean, the standard deviation, and so on) is equal to a hypothesized value. The null hypothesis is often an initial claim that is based on previous analyses or specialized knowledge.
- Alternative hypothesis
- The alternative hypothesis states that a population parameter is smaller, larger, or different from the hypothesized value in the null hypothesis. The alternative hypothesis is what you might believe to be true or hope to prove true.
Interpretation
In the output, the null and alternative hypotheses help you to verify that you entered the correct value for the hypothesized ratio.
Significance level
The significance level (denoted as α or alpha) is the maximum acceptable level of risk for rejecting the null hypothesis when the null hypothesis is true (type I error). Usually, you choose the significance level before you analyze the data. In Minitab, you can choose the significance level by specifying the confidence level, because the significance level equals 1 minus the confidence level. Because the default confidence level in Minitab is 0.95, the default significance level is 0.05.
Interpretation
Compare the significance level to the p-value to decide whether to reject or fail to reject the null hypothesis (H0). If the p-value is less than the significance level, the usual interpretation is that the results are statistically significant, and you reject H0.
- Choose a higher significance level, such as 0.10, to be more certain that you detect any difference that possibly exists. For example, a quality engineer compares the stability of new ball bearings with the stability of current bearings. The engineer must be highly certain that the new ball bearings are stable because unstable ball bearings could cause a disaster. The engineer chooses a significance level of 0.10 to be more certain of detecting any possible difference in stability of the ball bearings.
- Choose a lower significance level, such as 0.01, to be more certain that you detect only a difference that actually exists. For example, a scientist at a pharmaceutical company must be very certain about a claim that the company's new drug significantly reduces symptoms. The scientist chooses a significance level of 0.001 to be more certain that any significant difference in symptoms does exist.
N
The sample size (N) is the total number of observations in the sample.
Interpretation
The sample size affects the confidence interval and the power of the test.
Usually, a larger sample size results in a narrower confidence interval. A larger sample size also gives the test more power to detect a difference. For more information, go to What is power?.
StDev
The standard deviation is the most common measure of dispersion, or how spread out the data are about the mean. The symbol σ (sigma) is often used to represent the standard deviation of a population, while s is used to represent the standard deviation of a sample. Variation that is random or natural to a process is often referred to as noise.
The standard deviation uses the same units as the data.
Interpretation
The standard deviation of each sample is an estimate of each population standard deviation. Minitab uses the standard deviation to estimate the ratio in population standard deviations. You should concentrate on this ratio.
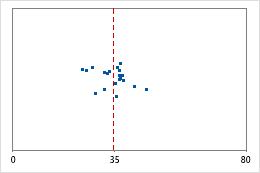
Hospital 1
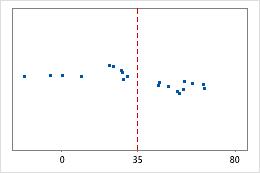
Hospital 2
Hospital discharge times
Administrators track the discharge time for patients who are treated in the emergency departments of two hospitals. Although the average discharge times are about the same (35 minutes), the standard deviations are significantly different. The standard deviation for hospital 1 is about 6. On average, a patient's discharge time deviates from the mean (dashed line) by about 6 minutes. The standard deviation for hospital 2 is about 20. On average, a patient's discharge time deviates from the mean (dashed line) by about 20 minutes.
Variance
The variance measures how spread out the data are about their mean. The variance is equal to the standard deviation squared.
Interpretation
The variance of each sample is an estimate of each population variance. Minitab uses the variances to estimate the ratio in population variances. You should concentrate on this ratio.
Estimated Ratio of standard deviations
The ratio of standard deviations is the standard deviation of the first sample divided by the standard deviation of the second sample.
Interpretation
The estimated ratio of standard deviations of your sample data is an estimate of the ratio in population standard deviations.
Because the estimated ratio is based on sample data and not on the entire population, it is unlikely that the sample ratio equals the population ratio. To better estimate the ratio, use the confidence interval.
Estimated Ratio of variances
The ratio of variances is the variance of the first sample divided by the variance of the second sample.
Interpretation
The estimated ratio of variances of your sample data is an estimate of the ratio in population variances.
Because the estimated ratio is based on sample data and not on the entire population, it is unlikely that the sample ratio equals the population ratio. To better estimate the ratio, use the confidence interval.
Confidence interval (CI) and bounds
The confidence interval provides a range of likely values for the population ratio. Because samples are random, two samples from a population are unlikely to yield identical confidence intervals. But, if you repeated your sample many times, a certain percentage of the resulting confidence intervals or bounds would contain the unknown population ratio. The percentage of these confidence intervals or bounds that contain the ratio is the confidence level of the interval. For example, a 95% confidence level indicates that if you take 100 random samples from the population, you could expect approximately 95 of the samples to produce intervals that contain the population ratio.
An upper bound defines a value that the population ratio is likely to be less than. A lower bound defines a value that the population ratio is likely to be greater than.
The confidence interval helps you assess the practical significance of your results. Use your specialized knowledge to determine whether the confidence interval includes values that have practical significance for your situation. If the interval is too wide to be useful, consider increasing your sample size. For more information, go to Ways to get a more precise confidence interval.
By default, the 2 variances test displays the results for Levene's method and Bonett's method. Bonett's method is usually more reliable than Levene's method. However, for extremely skewed and heavy tailed distributions, Levene's method is usually more reliable than Bonett's method. Use the F-test only if you are certain that the data follow a normal distribution. Any small deviation from normality can greatly affect the F-test results. For more information, go to Should I use Bonett's method or Levene's method for 2 Variances?.
Ratio of Standard Deviations
| Estimated Ratio | 95% CI for Ratio using Bonett | 95% CI for Ratio using Levene |
|---|---|---|
| 0.658241 | (0.372, 1.215) | (0.378, 1.296) |
In these results, the estimate for the population ratio of standard deviations for ratings from two hospitals is 0.658. Using Bonett's method, you can be 95% confident that the population ratio of the standard deviations for the hospital ratings is between 0.372 and 1.215.
DF
The degrees of freedom (DF) are the amount of information your data provide that you can "spend" to estimate the values of unknown population parameters, and calculate the variability of these estimates. For a 2 variances test, the degrees of freedom are determined by the number of observations in your sample and also depend on the method that Minitab uses.
Interpretation
Minitab uses the degrees of freedom to determine the test statistic. The degrees of freedom are determined by the sample size. Increasing your sample size provides more information about the population, which increases the degrees of freedom.
Test statistic for Bonett's method
The test statistic is a statistic that Minitab calculates for Bonett's method by inverting the confidence interval. The test statistic for Bonett's method is not available for summarized data or for data that are not balanced.
Interpretation
You can compare the test statistic to critical values of the chi-square distribution to determine whether to reject the null hypothesis. However, using the p-value of the test to make the same determination is usually more practical and convenient. The p-value has the same meaning for any size test, but the same chi-square statistic can indicate opposite conclusions depending on the sample size.
- For a two-sided test, the critical values are
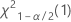 and
and  . If the test statistic is less than the first value or greater than the second value, you reject the null hypothesis. If the test statistic is between the first and second values, you fail to reject the null hypothesis.
. If the test statistic is less than the first value or greater than the second value, you reject the null hypothesis. If the test statistic is between the first and second values, you fail to reject the null hypothesis. - For a one-sided test with an alternative hypothesis of less than, the critical value is
 . If the test statistic is less than the critical value, you reject the null hypothesis. If it is not, you fail to reject the null hypothesis.
. If the test statistic is less than the critical value, you reject the null hypothesis. If it is not, you fail to reject the null hypothesis. - For a one-sided test of greater than, the critical value is
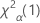 . If the test statistic is greater than the critical value, you reject the null hypothesis. If it is not, you fail to reject the null hypothesis.
. If the test statistic is greater than the critical value, you reject the null hypothesis. If it is not, you fail to reject the null hypothesis.
The test statistic is used to calculate the p-value.
Test statistic for Levene's method
The test use the one-way ANOVA F-statistic applied to the absolute median deviation of the observations. Therefore, applying Levene's method is equivalent to applying the one-way ANOVA procedure to the absolute median deviation of the observations. For 2-sample problems this method is also equivalent to applying the 2-sample t procedure to the absolute median deviation of the observations.
Interpretation
You can compare the test statistic to critical values of the F-distribution to determine whether to reject the null hypothesis. However, using the p-value of the test to make the same determination is usually more practical and convenient.
- For a two-sided test, the critical values are
 and
and 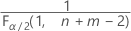 . If the test statistic is less than the first value or greater than the second value, you reject the null hypothesis. If the test statistic is between the first and second values, you fail to reject the null hypothesis.
. If the test statistic is less than the first value or greater than the second value, you reject the null hypothesis. If the test statistic is between the first and second values, you fail to reject the null hypothesis. - For a one-sided test with an alternative hypothesis of less than, the critical value is
 . If the test statistic is less than the critical value, you reject the null hypothesis. If it is not, you fail to reject the null hypothesis.
. If the test statistic is less than the critical value, you reject the null hypothesis. If it is not, you fail to reject the null hypothesis. - For a one-sided test of greater than, the critical value is
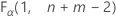 . If the test statistic is greater than the critical value, you reject the null hypothesis. If it is not, you fail to reject the null hypothesis.
. If the test statistic is greater than the critical value, you reject the null hypothesis. If it is not, you fail to reject the null hypothesis.
The test statistic is used to calculate the p-value.
Test statistic for the F method
The test statistic is a statistic for F-tests that measures the ratio between the observed variances.
Interpretation
You can compare the test statistic to critical values of the F-distribution to determine whether to reject the null hypothesis. However, using the p-value of the test to make the same determination is usually more practical and convenient.
- For a two-sided test, the critical values are
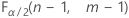 and
and 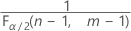 . If the test statistic is less than the first value or greater than the second value, you reject the null hypothesis. If the test statistic is between the first and second values, you fail to reject the null hypothesis.
. If the test statistic is less than the first value or greater than the second value, you reject the null hypothesis. If the test statistic is between the first and second values, you fail to reject the null hypothesis. - For a one-sided test with an alternative hypothesis of less than, the critical value is
 . If the test statistic is less than the critical value, you reject the null hypothesis. If it is not, you fail to reject the null hypothesis.
. If the test statistic is less than the critical value, you reject the null hypothesis. If it is not, you fail to reject the null hypothesis. - For a one-sided test of greater than, the critical value is
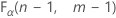 . If the test statistic is greater than the critical value, you reject the null hypothesis. If it is not, you fail to reject the null hypothesis.
. If the test statistic is greater than the critical value, you reject the null hypothesis. If it is not, you fail to reject the null hypothesis.
The test statistic is used to calculate the p-value.
P-Value
The p-value is a probability that measures the evidence against the null hypothesis. A smaller p-value provides stronger evidence against the null hypothesis.
Interpretation
Use the p-value to determine whether the difference in population standard deviations or variances is statistically significant.
- P-value ≤ α: The ratio of the standard deviations or variances is statistically significant (Reject H0)
- If the p-value is less than or equal to the significance level, the decision is to reject the null hypothesis. You can conclude that the ratio of the population standard deviations or variances is not equal to the hypothesized ratio. If you did not specify a hypothesized ratio, Minitab tests whether no difference between the standard deviations or variances (Hypothesized ratio = 1) exists. Use your specialized knowledge to determine whether the difference is practically significant. For more information, go to Statistical and practical significance.
- P-value > α: The ratio of the standard deviations or variances is not statistically significant (Fail to reject H0)
- If the p-value is greater than the significance level, the decision is to fail to reject the null hypothesis. You do not have enough evidence to conclude that the ratio of the population standard deviations or variances is statistically significant. You should make sure that your test has enough power to detect a difference that is practically significant. For more information, go to Power and Sample Size for 2 Variances.
- Bonett's test is accurate for any continuous distribution and does not require that the data are normal. Bonett's test is usually more reliable than Levene's test.
- Levene's test is also accurate with any continuous distribution. For extremely skewed and heavy tailed distributions, Levene's method tends to be more reliable than Bonett's method.
- The F-test is accurate only for normally distributed data. Any small deviation from normality can cause the F-test to be inaccurate, even with large samples. However, if the data conform well to the normal distribution, then the F-test is usually more powerful than either Bonett's test or Levene's test.
For more information, go to Should I use Bonett's method or Levene's method for 2 Variances?.
Summary plot
The summary plot shows confidence intervals for the ratio and confidence intervals for the standard deviations or variances of each sample. The summary plot also shows boxplots of the sample data and p-values for the hypothesis tests.
Confidence intervals
The confidence interval provides a range of likely values for the population ratio. Because samples are random, two samples from a population are unlikely to yield identical confidence intervals. But, if you repeated your sample many times, a certain percentage of the resulting confidence intervals or bounds would contain the unknown population ratio. The percentage of these confidence intervals or bounds that contain the ratio is the confidence level of the interval. For example, a 95% confidence level indicates that if you take 100 random samples from the population, you could expect approximately 95 of the samples to produce intervals that contain the population ratio.
An upper bound defines a value that the population ratio is likely to be less than. A lower bound defines a value that the population ratio is likely to be greater than.
Interpretation
The confidence interval helps you assess the practical significance of your results. Use your specialized knowledge to determine whether the confidence interval includes values that have practical significance for your situation. If the interval is too wide to be useful, consider increasing your sample size. For more information, go to Ways to get a more precise confidence interval.
By default, the 2 variances test displays the results for Levene's method and Bonett's method. Bonett's method is usually more reliable than Levene's method. However, for extremely skewed and heavy tailed distributions, Levene's method is usually more reliable than Bonett's method. Use the F-test only if you are certain that the data follow a normal distribution. Any small deviation from normality can greatly affect the F-test results. For more information, go to Should I use Bonett's method or Levene's method for 2 Variances?.
Boxplot
A boxplot provides a graphical summary of the distribution of each sample. The boxplot makes it easy to compare the shape, the central tendency, and the variability of the samples.
Interpretation
Use a boxplot to examine the spread of the data and to identify any potential outliers. Boxplots are best when the sample size is greater than 20.
- Skewed data
-
Examine the spread of your data to determine whether your data appear to be skewed. When data are skewed, the majority of the data are located on the high or low side of the graph. Often, skewness is easiest to detect with a histogram or boxplot.
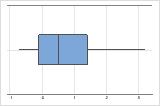
Right-skewed
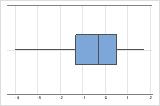
Left-skewed
The boxplot with right-skewed data shows wait times. Most of the wait times are relatively short, and only a few wait times are long. The boxplot with left-skewed data shows failure time data. A few items fail immediately, and many more items fail later.
Data that are severely skewed can affect the validity of the p-value if your sample is small (either sample is less than 20 values). If your data are severely skewed and you have a small sample, consider increasing your sample size.
- Outliers
-
Outliers, which are data values that are far away from other data values, can strongly affect the results of your analysis. Often, outliers are easiest to identify on a boxplot.
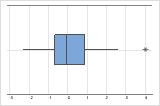
On a boxplot, asterisks (*) denote outliers.
Try to identify the cause of any outliers. Correct any data–entry errors or measurement errors. Consider removing data values for abnormal, one-time events (also called special causes). Then, repeat the analysis. For more information, go to Identifying outliers.
Individual value plot
An individual value plot displays the individual values in each sample. An individual value plot makes it easy to compare the samples. Each circle represents one observation. An individual value plot is especially useful when you have relatively few observations and when you also need to assess the effect of each observation.
Interpretation
Use an individual value plot to examine the spread of the data and to identify any potential outliers. Individual value plots are best when the sample size is less than 50.
- Skewed data
-
Examine the spread of your data to determine whether your data appear to be skewed. When data are skewed, the majority of the data are located on the high or low side of the graph. Often, skewness is easiest to detect with a histogram or boxplot.
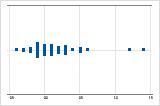
Right-skewed
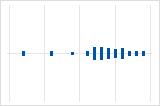
Left-skewed
The individual value plot with right-skewed data shows wait times. Most of the wait times are relatively short, and only a few wait times are long. The individual value plot with left-skewed data shows failure time data. A few items fail immediately, and many more items fail later.
Data that are severely skewed can affect the validity of the p-value if your sample is small (either sample is less than 20 values). If your data are severely skewed and you have a small sample, consider increasing your sample size.
- Outliers
-
Outliers, which are data values that are far away from other data values, can strongly affect the results of your analysis. Often, outliers are easiest to identify on a boxplot.
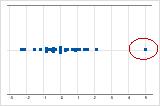
On an individual value plot, unusually low or high data values indicate possible outliers.
Try to identify the cause of any outliers. Correct any data–entry errors or measurement errors. Consider removing data values for abnormal, one-time events (also called special causes). Then, repeat the analysis. For more information, go to Identifying outliers.
Histogram
A histogram divides sample values into many intervals and represents the frequency of data values in each interval with a bar.
Interpretation
Use a histogram to assess the shape and spread of the data. Histograms are best when the sample size is greater than 20.
- Skewed data
-
Examine the spread of your data to determine whether your data appear to be skewed. When data are skewed, the majority of the data are located on the high or low side of the graph. Often, skewness is easiest to detect with a histogram or boxplot.
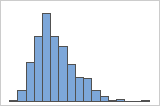
Right-skewed
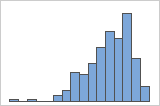
Left-skewed
The histogram with right-skewed data shows wait times. Most of the wait times are relatively short, and only a few wait times are long. The histogram with left-skewed data shows failure time data. A few items fail immediately, and many more items fail later.
Data that are severely skewed can affect the validity of the p-value if your sample is small (either sample is less than 20 values). If your data are severely skewed and you have a small sample, consider increasing your sample size.
- Outliers
-
Outliers, which are data values that are far away from other data values, can strongly affect the results of your analysis. Often, outliers are easiest to identify on a boxplot.
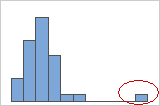
On a histogram, isolated bars at either ends of the graph identify possible outliers.
Try to identify the cause of any outliers. Correct any data–entry errors or measurement errors. Consider removing data values for abnormal, one-time events (also called special causes). Then, repeat the analysis. For more information, go to Identifying outliers.
