Methods and formulas for 1-Sample Poisson Rate

Select the method or formula of your choice.

In This Topic

Statistics
P-value for exact test
Confidence intervals and confidence bounds for exact test
P-value for normal approximation
Confidence intervals and confidence bounds for normal approximation

Statistics

Minitab generates the following descriptive statistics from your sample. Minitab displays a mean only if you change "length" from its default value of 1.

Term	Description
rate of occurrence
mean occurrence

The rate equals the average number of occurrences per unit length of observation. The mean is the average number of occurrences in the entire sample. If length equals 1, then rate and mean are equal.

P-value for exact test

Formula

The exact test for 1-Sample Poisson Rate uses the following equations to calculate p-values for the respective alternative hypotheses:

H₁: λ > λ₀: p-value = P(S ≥ s | λ = λ₀) where S has a Poisson distribution with mean nλ₀t.
H₁: λ < λ₀: p-value = P(S ≤ s | λ = λ₀) where S has a Poisson distribution with mean nλ₀t.
H₁: λ ≠ λ₀: Minitab uses a likelihood ratio test as follows:
Define the function G(s), which expresses the likelihood ratio test in terms of s, the total number of occurrences in the Poisson process:
- if 0 ≤ s < nλ₀t, solve the equation G(y) = G(s) for y in the interval (nλ₀t, enλ₀t];
  p-value = P(S ≤ s | λ = λ₀) + P(S ≥ y | λ = λ₀)
- if s = nλ₀t, then
  p-value = 1.00
- if nλ₀t < s ≤ enλ₀t, solve the equation G(y) = G(s) for y in the interval [0, nλ₀t);
  p-value = P(S ≤ y | λ = λ₀) + P(S ≥ s | λ = λ₀)
- if s > enλ₀t, the test is one-sided, and
  p-value = P(S ≥ s | λ = λ₀)
where S has a Poisson distribution with mean nλ₀t.

Notation

Term	Description
s	total number of occurrences in the Poisson process
t	"length" of observation
λ₀	hypothesized value of the population rate paramter
λ	true value of the population rate parameter
n	sample size
e	2.71828, approximately

Confidence intervals and confidence bounds for exact test

Confidence intervals

An exact 100(1 – α)% confidence interval for the occurrence rate of a Poisson process is given by:

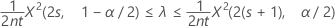
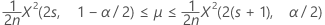
When you specify a value of "length", Minitab also displays a confidence interval for the mean number of occurrences. That confidence interval given by:

Confidence bounds

When you specify a one-sided test, Minitab calculates a one-sided 100(1 – α)% confidence bound, according to the direction of the alternative hypothesis.

If you specify a "greater than" alternative hypothesis, the exact 100(1 – α)% lower bound of the rate is given by:

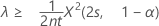
The exact 100(1 – α)% lower bound of the mean is given by:
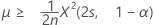
If you specify a "less than" alternative hypothesis, the exact 100(1 – α)% upper bound of the rate is given by:

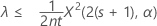
The exact 100(1 – α)% upper bound of the mean is given by:

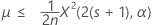
Notation

Term	Description
s	total number of occurrences in the Poisson process
t	"length" of observation
λ	true value of the population rate
μ	true value of the population mean
Χ²_{(p, x)}	upper x percentile point of the Χ² distribution with p degrees of freedom, where 0 < x < 1.
α	alpha-level for the 100(1–α)% confidence interval
n	sample size

P-value for normal approximation

Normal approximations are valid if the total number of occurrences is greater than 10.

Formula

The hypothesis test based on a normal approximation for 1-Sample Poisson Rate uses the following p-value equations for the respective alternative hypotheses:

Notation

Term	Description
Z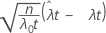
t	"length" of observation
λ ₀	hypothesized value of the population rate parameter
λ	true value of the population rate parameter
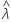	observed value of the sample rate statistic
n	sample size

Confidence intervals and confidence bounds for normal approximation

Confidence intervals

An 100(1 – α)% confidence interval, based on a normal approximation, for the occurrence rate of a Poisson process is given by:

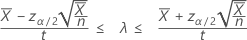
When you specify a value of "length", Minitab also displays a confidence interval for the mean number of occurrences. That confidence interval is given by:

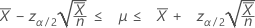
Confidence bounds

When you specify a one-sided test, Minitab calculates a one-sided 100(1 – α)% confidence bound, according to the direction of the alternative hypothesis.

If you specify a "greater than" alternative hypothesis, the exact 100(1 – α)% lower bound of the rate is given by:

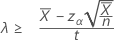
If you specify a value of "length", the exact 100(1-α)% lower bound of the mean is given by:
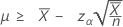
If you specify a "less than" alternative hypothesis, the exact 100(1 – α)% upper bound of the rate is given by:

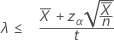
If you specify a value of "length", the exact 100(1 – α)% upper bound of the mean is given by:

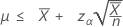
Notation

Term	Description
s	total number of occurrences in the Poisson process
t	"length" of observation
λ	true value of the population rate
μ	true value of the population mean
Z_x	upper x percentile point of the standard normal distribution, where 0 < x < 1.
α	alpha-level for the 100(1–α)% confidence interval
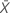	mean number of occurrences in the sample
n	sample size