Winters' method employs a level component, a trend component, and a seasonal component at each period. It uses three weights, or smoothing parameters, to update the components at each period. Initial values for the level and trend components are obtained from a linear regression on time. Initial values for the seasonal component are obtained from a indicator variable regression using detrended data. The following equations are the Winters' method smoothing equations.
Smoothing equation for the additive model
- Lt= α (Yt - St-p) + (1 - α) [Lt-1 + Tt-1]
- Tt = γ [Lt - Lt-1] + (1 - γ)Tt-1
- St = δ (Yt - Lt) + (1 - δ) St-p
= Lt-1 + Tt-1 + St-p
Smoothing equation for the multiplicative model
- Lt= α (Yt / St-p) + (1 - α) [Lt-1 + Tt-1]
- Tt = γ [Lt - Lt-1] + (1 - γ)Tt-1
- St = δ (Yt / Lt) + (1 - δ) St-p
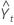= (Lt-1 + Tt-1) St-p
Notation
| Term | Description |
|---|---|
| Lt | The level at time t |
| α | The weight for the level |
| Tt | The trend at time t |
| γ | The weight for the trend |
| St | The seasonal component at time t |
| δ | The weight for the seasonal component |
| p | The seasonal period |
| Yt | The data value at time t |
 | The fitted value, or one-period-ahead forecast, at time t |
