Lag
The lag is the number of time periods that separate the two time series. The default number of lags ranges from (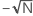
+ 10) to (
+ 10).
Cross Correlation Function (CCF)
The cross correlation function is the correlation between the observations of two time series xt and yt, separated by k time units (the correlation between yt+k and xt).
Interpretation
Use the cross correlation function to determine whether there is a relationship between two time series. To determine whether a relationship exists between the two series, look for a large correlation, with the correlations on both sides that quickly become non-significant. Usually, a correlation is significant when the absolute value is greater than 
, where n is the number of observations and k is the lag. This calculation is a rule of thumb procedure based on large-sample normal approximation. If the population cross correlation of lag k is zero for k=1, 2, ... then, for fairly large n, rxy(k) will be approximately normally distributed, with mean (μ) zero and standard deviation (σ) 1/
. Since approximately 95% of a normal population is within 2 standard deviations of the mean, a test that rejects the hypothesis that the population cross correlation of lag k equals zero when |rxy(k) | is greater than 2/
has a significance level (α) of approximately 5%.
Note
The interpretation for the cross correlation function depend on the assumption that there is no autocorrelation. For more information, go to Look for evidence of autocorrelation.
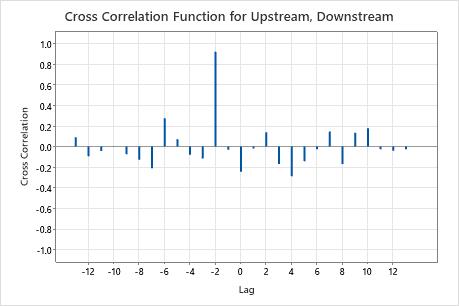
On this plot, the correlation at lag −2 is approximately 0.92. Because 0.92 > 0.5547 = 
the correlation is significant. You can conclude that the water moves from the upstream location to the downstream location in two days.
