In This Topic
Box-Cox transformation
The Box-Cox transformation is given by the following formula:
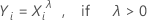
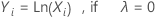

where Xi is an original data value and λ is the parameter for the transformation. When the analysis searches for the optimal value of λ, the analysis rounds the optimal value of λ to 0.5 or to the nearest integer to perform the transformation.
Common λ values
| λ | Transformation |
|---|---|
| 2 | 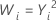 |
| 0.5 |  |
| 0 |  |
| −1 |  |
Search for the optimal λ
- Define the criterion for the optimal value to be a minimum coefficient of variation.
- Divide the series into H sub-series.
- Use the method from Brent to find the value of λ that minimizes the coefficient of variation.
The following sections define the sub-series and the coefficient of variation.
Sub-series
Divide the series into sub-series by seasonal period. If the seasonal period does not divide evenly into the series, omit the remaining observations from the beginning of the series. If the specifications for the analysis do not include a seasonal period, then set the seasonal period = 2.
For example, assume an original time series with 10 observations and a seasonal period of 4: {5, 6, 3, 2, 9, 8, 1, 7, 10, 4}. The number of sub-series is 10 modulo 4 = 2. Because 4 does not divide evenly into 10, use only the last 8 observations to form the sub-series. The sub-series are {3, 2, 9, 8} and {1, 7, 10, 4}.
Missing values
If a sub-series contains 1 or more missing values, omit the sub-series from the calculations in the search for the optimal value of λ. The search requires at least 2 sub-series with no missing values.
Coefficient of variation
Use the following definitions to calculate the coefficient of variation:| Term | Description |
|---|---|
| X1, X2, … XN | the observations in the original time series |
| P | the seasonal period of the original time series |
| Xh, i | the ith observation in subseries h, where i=1, …, P and h=1, …, H |
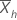 | the sample mean of the hth sub-series |
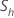 | the sample standard deviation of the hth sub-series |
The following equations define the statistics for each sub-series:
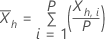
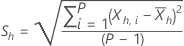
For a given λ and for h=1, …, H use the following definition:
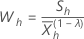
Calculate the sample average and the sample standard deviation for the W statistics:

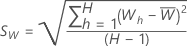

Use the method from Brent to find the value of λ that minimizes the CV in the interval from the specifications for the analysis. The analysis rounds the optimal value of λ to 0.5 or to the nearest integer to perform the transformation.
