Lognormal distribution in reliability analysis

In This Topic

Uses of the lognormal distribution to model reliability data
Probability density function and hazard function for the lognormal distribution

Uses of the lognormal distribution to model reliability data

The lognormal distribution is a flexible distribution that is closely related to the normal distribution. This distribution can be especially useful for modeling data that are roughly symmetric or skewed to the right. Like the Weibull distribution, the lognormal distribution can have markedly different appearances depending on its scale parameter.

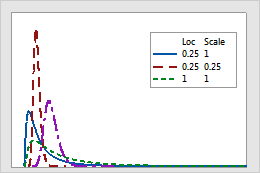
In fact, the lognormal model and the Weibull model may sometimes fit a specific set of life test data equally well. However, there is one important difference to consider. When using these distributions to extrapolate beyond the range of sample data, the lognormal will predict lower average failure rates at earlier times than the Weibull distribution.

The lognormal distribution has been called the most commonly used life distribution model for many high-technology applications. The distribution is based on the multiplicative growth model, which means that at any instant of time, the process undergoes a random increase of degradation that is proportional to its current state. The multiplicative effect of all these random independent growths accumulates to trigger failure. Therefore, the distribution is often used to model parts or components that fail primarily due to stress or fatigue, including the following applications:

Failure due to chemical reactions or degradation, such as corrosion, migration, or diffusion, which is common with semiconductor failure
Time to fracture in metals subject to the growth of fatigue cracks
Electronic components that exhibit decreased risk of failure after a certain time

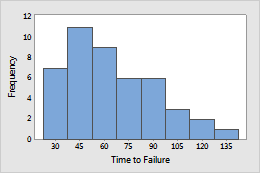
However, if components are not expected to fail until well after the technological life of the product in which they are installed is complete (that is, the failure rate of a component is constant during its expected lifetime), an exponential distribution may be more appropriate.

Example 1: Electronic components

Engineers record the time to failure of an electronic component under normal operating conditions. The component shows a decreased risk of failure over time which could be modeled using a lognormal distribution.

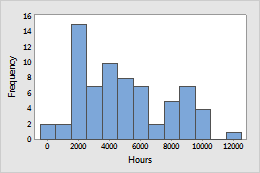
Example 2: Diesel generator fans

Time until failure was tracked during the life of diesel generator fans. A lognormal distribution was used to model the data.

Probability density function and hazard function for the lognormal distribution

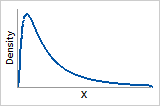
Probability density function
The data are skewed to the right.

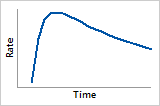
Hazard function
The risk of failure quickly increases to a maximum, then decreases.