Point estimate of a percentile for a given percent
The pth percentile point, xp, is the stress level needed for a response p.
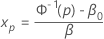
To find the estimate of xp, use the following formula:
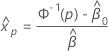
where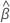 
and 
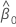are the maximum likelihood estimates of 
and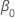 
.
Log-location distributions for Probit Analysis are the lognormal, loglogistic, and Weibull distributions. For log-location distributions, the previous formulas estimate the percentile on the log scale. To estimate the percentile on the scale of the data with these distributions, use the following formula.
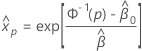
Standard error of a percentile for a given percent
The calculation of the standard error of a percentile uses the delta method. The standard error of the estimated percentile has the following formula.
where the variance of 
has the following form:
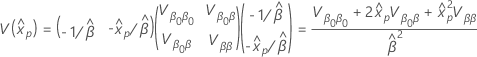
and the variance-covariance matrix of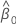 
and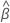 
has the following form:
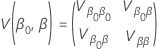
Log-location distributions for Probit Analysis are the lognormal, loglogistic, and
Weibull distributions. For log-location distributions, the previous formulas
estimate the variance of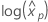 
. Definitions of the variance and the variance-covariance matrix in
terms of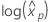 
follow.
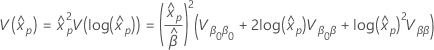
Fiducial confidence interval of a percentile for a given percent
The two-sided, 100(1 - 
) for 
is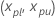 
with the following equations.
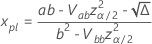
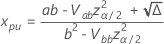
where
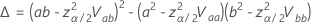
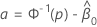
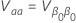
Log-location distributions for Probit Analysis are the lognormal, loglogistic, and Weibull distributions. For log-location distributions, the previous formulas estimate the interval on the log scale. To estimate the interval on the scale of the data, exponentiate the confidence limits in the previous formulas.
Fiducial confidence interval of the failure probability or the survival probability at a given stress value
The two-sided, 100(1 - 
) for the failure probability,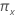 
, is 
. For the survival probability, 
, the interval is 
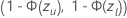. The following formulas give the calculations.
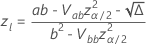
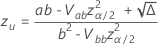
where
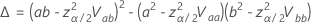
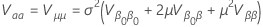
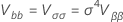
and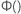 
is the cumulative distribution function of the distribution for
the analysis.
Log-location distributions for Probit Analysis are the lognormal, loglogistic, and Weibull distributions. For log-location distributions, substitute the following definition.
References
The derivation of the fiducial confidence intervals uses Fieller's theorem. Fieller's theorem is in the following reference.
Finney, D. J. (1971). Probit analysis, (Third edition), London: Cambridge University Press.
For more information on the probit model and the estimation of percentiles, consult the following reference.
Cox, D. R. and Snell, E. J. (1989). The analysis of binary data (Second edition), London: Chapman & Hall.
