In This Topic
Two distributional parameters specified
If you specify the planning values for both μ and σ (θ and β for the Weibull model), then Minitab calculates the percentile or the reliability.
- The planning value for the pth percentile is calculated as follows:
- for location-scale models (normal, logistic and extreme value)

- for log-location-scale models (Weibull, lognormal, loglogistic)
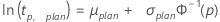
- for location-scale models (normal, logistic and extreme value)
- The planning value for reliability at a given time is calculated as follows:
- for location-scale models (normal, logistic, extreme value)
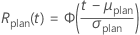
- for log-location-scale models (Weibull, lognormal, loglogistic)

- for location-scale models (normal, logistic, extreme value)
Notation
| Term | Description |
|---|---|
| μ | mean (normal, logistic), location (smallest extreme value), or log-location (lognormal, loglogistic) |
| σ | scale parameter |
| θ | scale parameter for Weibull |
| β | shape parameter for Weibull |
| t | time |
| tp,plan | planning value for the pth percentile at time t |
| Rplan(t) | planning value for reliability at time t |
| Φ | CDF for the corresponding distribution |
| Φ-1 | inverse CDF for the corresponding distribution |
Percentile and shape (or scale) specified
If you specify the planning values for β (or σ) and a percentile tp0, then Minitab calculates the planning value for μ as follows:
- For location-scale models (normal, logistic and extreme value)
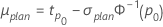
- For log-location-scale models (Weibull, lognormal and loglogistic)

To obtain the planning value for the percentile or the reliability, use the calculations for when two parameters are specified. For more information, see the section "Two distributional parameters specified".
Notation
| Term | Description |
|---|---|
| μ | mean (normal, logistic), location (smallest extreme value), or log-location (lognormal, loglogistic) |
| μplan | planning value for mean (normal, logistic), location (smallest extreme value), or log-location (lognormal, loglogistic) |
| σ | scale parameter |
| σplan | planning value for scale parameter |
| β | shape parameter for Weibull |
| t | time |
| tp | percentile at time t |
| Φ-1 | inverse CDF for the corresponding distribution |
Percentile and scale (or location) specified
If you specify the planning values for μ (or θ) and a percentile tp0 then Minitab calculates the planning value for σ as follows:
- For location-scale models (normal, logistic and extreme value)
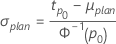
- For log-location-scale models (Weibull, lognormal and loglogistic)

To obtain the planning value for the percentile or the reliability, use the calculations for when two parameters are specified. For more information, see the section "Two distributional parameters specified".
Notation
| Term | Description |
|---|---|
| μ | mean (normal, logistic), location (smallest extreme value), or log-location (lognormal, loglogistic) |
| μplan | planning value for mean (normal, logistic), location (smallest extreme value), or log-location (lognormal, loglogistic) |
| σ | scale parameter |
| σplan | planning value for scale parameter |
| β | shape parameter for Weibull |
| t | time |
| tp | percentile at time t |
| Φ-1 | inverse CDF for the corresponding distribution |
Two percentiles specified
If you specify the planning values for two percentiles, then Minitab calculates the planning values for both μ and σ.
- The planning value for μ is calculated as follows:
- For location-scale models (normal, logistic and extreme value)
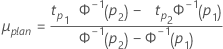
- For log-location-scale models (Weibull, lognormal, loglogistic)
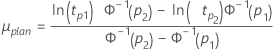
- For location-scale models (normal, logistic and extreme value)
- The planning value for σ is calculated as follows:
- For location-scale models (normal, logistic, extreme value)
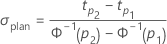
- For log-location-scale models (Weibull, lognormal, loglogistic)
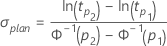
- For location-scale models (normal, logistic, extreme value)
To obtain the planning value for the percentile or the reliability, use the calculations for when two parameters are specified. For more information, see the section "Two distributional parameters specified".
Notation
| Term | Description |
|---|---|
| μ | mean (normal, logistic), location (smallest extreme value), or log-location (lognormal, loglogistic) |
| μplan | planning value for mean (normal, logistic), location (smallest extreme value), or log-location (lognormal, loglogistic) |
| σ | scale parameter |
| σplan | planning value for scale parameter |
| β | shape parameter for Weibull |
| t | time |
| tp | percentile at time t |
| Φ-1 | inverse CDF for the corresponding distribution |
