In This Topic
Pdf and cdf
The probability density function (pdf) and cumulative distribution function (cdf) for each reliability distribution are as follows:
Smallest extreme value
-

- cdf
-

Weibull
-
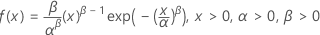
- cdf
-

3-parameter Weibull
-
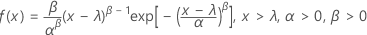
- cdf
-

Exponential
-
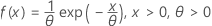
- cdf
-

2-parameter exponential
-
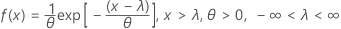
- cdf
-
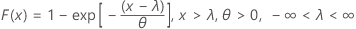
Normal
-
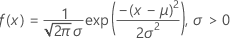
- cdf
-
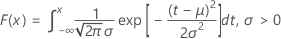
Lognormal
-
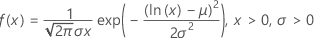
- cdf
-

3-parameter lognormal
-

- cdf
-

Logistic
-
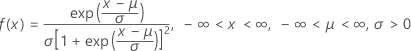
- cdf
-

Loglogistic
-
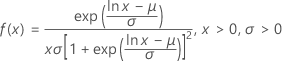
- cdf
-

3-parameter loglogistic
-
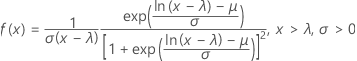
- cdf
-

For more information on distribution parameters, see the section "Parameter estimates".
Notation
| Term | Description |
|---|---|
| μ | location parameter |
| σ | scale parameter (Weibull and 3-parameter Weibull) |
| θ | scale parameter (smallest extreme value, exponential, and 2-parameter exponential) |
| α | scale parameter (other distributions) |
| β | shape parameter |
| λ | threshold parameter |
Hazard function
The hazard function provides a measure of the likelihood of failure as a function of how long a unit has survived (the instantaneous failure rate at a particular time, t).
Formula
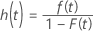
Notation
| Term | Description |
|---|---|
| f(t) | pdf of the chosen distribution |
| F(t) | cdf of the chosen distribution |
Relationships between distributions
When data follow a log-based distributions (Weibull, exponential, lognormal, loglogistic), sometimes calculations are simpler by first taking the log of your data and fitting the corresponding related distribution.
| If your data follow this distribution... | The log of your data will follow this distribution... |
|---|---|
| Weibull, exponential | Smallest extreme value |
| Lognormal | Normal |
| Loglogistic | Logistic |
