Survival probabilities
The reliability function R(t), also known as the survival function S(t), represents the probability a unit survives beyond time t.
Formula
R(t) = 1 - F(t)
The reliability of a series system is the product of the reliability functions of the components because all of the components must survive in order for the system to survive. To calculate the reliability of a series system of independent components, multiply the reliability functions of all the components together.
Notation
| Term | Description |
|---|---|
| F(t) | cdf for the chosen distribution |
Confidence limits for survival probabilities
The lower and upper confidence limits for the survival probabilities are defined by the following formulas:
Formula
where 
and 
(the variance of the survival probabilities) are defined as follows, based on the distribution.
Smallest extreme value, normal, lognormal, logistic, loglogistic
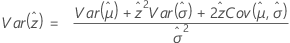
3-parameter lognormal, 3-parameter loglogistic
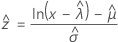
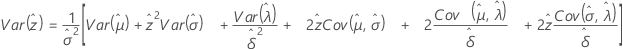
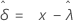
Weibull
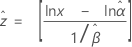
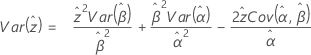
3-parameter Weibull
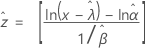
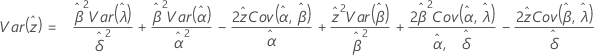
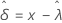
Exponential
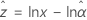
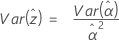
2-parameter exponential
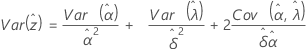
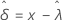
Notation
| Term | Description |
|---|---|
| zα | the 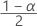 upper critical value for the standard normal distribution where 100α % is the confidence level. |
