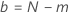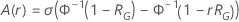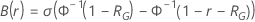The calculations for the probability of passing a test plan depend on the distribution that models the failures. For a log-location-scale distribution, the probability is a function of the ratio of improvement. For a location-scale distribution, the probability is a function of the amount of improvement. The expression of the formulas divides neatly into two cases that depend on whether you specify the sample size or the testing time.
Sample size
 confidence level satisfies the following equation:
confidence level satisfies the following equation: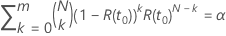
 ,
the solution,
,
the solution,  ,
of the equation has the following form:
,
of the equation has the following form: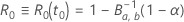
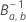 is the inverse cumulative distribution function of the beta distribution with
the following shape parameters:
is the inverse cumulative distribution function of the beta distribution with
the following shape parameters:
 ,
invert the function
,
invert the function  .
The inversion depends on the distribution family.
.
The inversion depends on the distribution family.
- Log-location-scale family

- Location-scale family
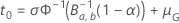
 and the improvement:
and the improvement: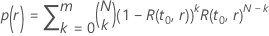
where 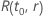 is the reliability function of the distribution model in terms of
is the reliability function of the distribution model in terms of
 and
and 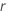 .
.
- Log-location-scale family

- Location-scale family
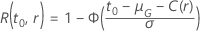
The following table gives the function of  for the distribution family and the goal of the test:
for the distribution family and the goal of the test:
| Reliability Goal | ||||
|---|---|---|---|---|
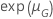
|

|
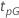
|

|
|
| Log-location-scale |  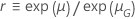 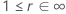 |
 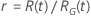  |
 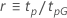 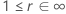 |
  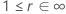 |
| Reliability Goal | ||||
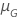
|

|
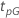
|

|
|
| Location-scale | 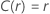  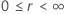 |
 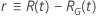  |
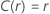  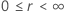 |
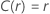 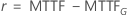 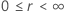 |
Example of 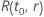 for the Weibull distribution
for the Weibull distribution
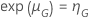 ,
and a given sample size, the probability of passing has the following form:
,
and a given sample size, the probability of passing has the following form:
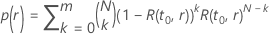
where

Testing time
 confidence level satisfies the following equation:
confidence level satisfies the following equation:
 ),
the solution of the equation,
),
the solution of the equation, 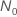 ,
has the following form:
,
has the following form:
 ),
no closed-form solution exists. Meeker and Escobar (1998)1 give the following approximate solution:
),
no closed-form solution exists. Meeker and Escobar (1998)1 give the following approximate solution: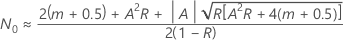
where

Minitab finds the exact solution numerically when
 .
.
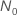 and the improvement:
and the improvement: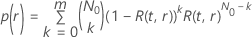
where 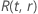 is the reliability function of the distribution model in terms of
is the reliability function of the distribution model in terms of
 and
and 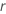 .
.
- Log-location-scale family

- Location-scale family
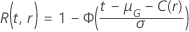
The function  has the same definitions as when the specifications for the test give the
sample size.
has the same definitions as when the specifications for the test give the
sample size.
Example of 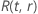 for the Weibull distribution
for the Weibull distribution
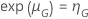 ,
and a given testing time, the probability of passing has the following form:
,
and a given testing time, the probability of passing has the following form:
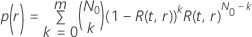
where

Notation
| Term | Description |
|---|---|
| N | sample size for the design when the specifications for the test provide the sample size |
| m | number of units that fail during the test |
 | significance level, such that the confidence level for the demonstration
test is 
|
 | scale parameter |
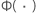 | cumulative distribution function of the standard distribution for the selected log-location-scale or location-scale distribution |
 | inverse cumulative distribution function of the standard distribution for the selected log-location-scale or location-scale distribution |
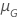 | location parameter for the distribution that meets the goal of the test |
 | shape parameter of the Weibull distribution |
 | testing time when the specifications for the test provide the sample size |
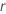 | ratio of improvement for log-location-scale distributions or the amount of improvement for location-scale distributions |
 | reliability at time t that is the goal for the test |
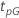 | percentile at percent p that is the goal for the test |
 | mean-time-to-failure that is the goal of the test |
 | testing time when the specifications for the test provide the testing time |
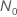 | sample size when the specification for the test provide the testing time |