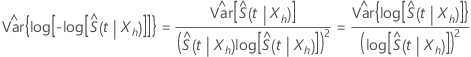In This Topic
Survival function
The survival function uses the following definitions:
| Term | Description |
|---|---|
 | the distinct, ordered, event times |
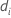 | the number of events at time  |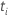
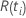 | the risk set at time  ,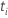
which is the set of all sample units that have yet to fail prior to time
 |
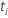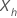 | the p-component vector of covariate values that represents a new or an existing data point |
Given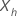 
,
the survival function for the Cox proportional hazards model has the following
form:
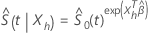
where
and
The function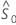 
estimates the survival function of an individual when the values of all the
covariates are 0. The function 
is the Breslow's estimator of the baseline cumulative hazard rate. The function
is a step function that jumps at the observed event times.
Confidence intervals
Under mild regularity conditions, the estimator
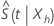has an asymptotic normal distribution with mean
and asymptotic variance with the following form:
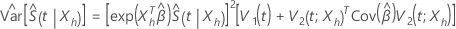
where
and
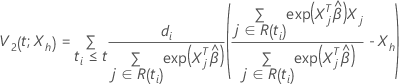
A direct Wald method confidence interval is available but is less accurate
because the distribution of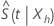 
is severely skewed. In addition, the confidence limits of such intervals are
often outside of the interval [0, 1]. The distribution of the logarithm of
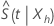is less skewed and converges more quickly to the normal distribution. Minitab
makes use of the following transformations to calculate the confidence
intervals.
Log transformation
Minitab calculates a confidence interval for
and back-transforms the confidence limits to provide the confidence interval
for 
.
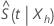Using this approach, an approximate 100(1 –
α) confidence interval for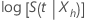 
has the following form:
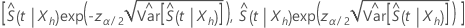
where 
estimates the asymptotic variance of 
and has the following form:
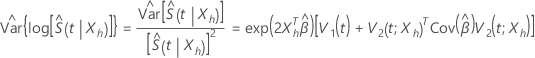
If the upper confidence limit for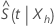 
exceeds 1, then Minitab uses 1 as the upper limit.
Log-log transformation
The log-log transformation guarantees that the confidence interval for
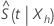is in the interval (0, 1). Minitab calculates a confidence interval for
and back-transforms the confidence limits to provide the confidence interval
for 
.
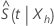Using this method, an approximate 100(1 –
α) confidence interval for 
has the following form:
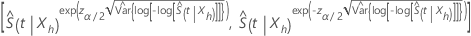
where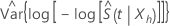 
estimates the asymptotic variance of 
and has the following form:
