Consider two individuals with risk vectors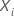 
and 
.
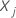The relative risk of the individuals is the ratio of the risks of the
individuals:
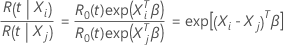
In the Cox proportional hazards model, the result of the ratio is a
constant. In particular, the relative risk does not depend on time,
t. This result makes the risks of two individuals proportional.
Relative risks for categorical predictors follow by changing the level of one
categorical predictor between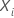 
and 
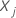while the values of the other predictors remain the same. Relative risks for
continuous predictors follow by changing the value of the continuous predictor
by a meaningful increment between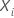 
and 
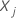while the values of the other predictors remain the same. For information on
the calculation of the coefficients and their standard errors, go to
Methods and formulas for the coefficients and regression equation for Fit Cox Model with Fixed Predictors only.
The relative risks provide an interpretation of the regression coefficients. The calculations and interpretation depend on if the predictor is categorical or continuous.
Relative risks for categorical predictors
For a categorical variable, the relative risk represents the comparison of the risk at one level of the variable to the risk at another level of the variable. The calculations assume that the values of the other predictors remain the same.
Let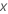 
represent a categorical predictor. Two levels of
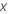have the following codes: 
and 
.
Let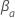 
be the regression coefficient for 
.
Let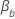 
be the coefficient for 
.
The estimated relative risk (RR) that compares
to 
has
the following form:
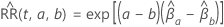
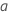and 
:
- For dummy coding,
and 
- For effect coding,
and 
| Dummy coding (0, 1) | Effect coding (-1, 0, 1) |
|---|---|
 |
 |
With dummy coding, the reference level always has the coefficient
.
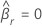Confidence interval
The 100(1 - 
)
confidence interval for the relative risk has the following form:
Relative risks for continuous predictors
Let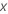 
be the observed value of a continuous predictor. The calculations assume that
the values of the other predictors remain the same. A change of
c units in the continuous predictor has the following relative risk:
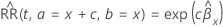
Confidence interval
The 100(1 - 
)
confidence interval for the relative risk has the following form:
