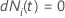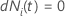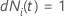| Term | Description |
|---|---|
 | the distinct, ordered, event times |
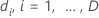 | the number of events at time 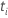
|
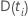 | the set of all units that experience the event at time
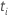 |
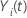 | an indicator variable that has the value 1 if subject
i is at risk at time
t and 0 otherwise, which is equivalent to
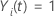 if
if 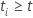 and
and 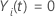 otherwise
otherwise |
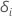 | an indicator for if subject
i is censored, such that  if subject
i experienced the event and
if subject
i experienced the event and 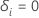 otherwise
otherwise |
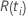 | the risk set at time 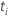 ,
which is the set of all sample units who have yet to fail prior to time ,
which is the set of all sample units who have yet to fail prior to time
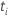 |
 | the number of events for subject i up to and including time t |
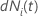 | the change in  for subject
i at time
t such that
for subject
i at time
t such that
|
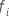 | the first event time at which subject i is in the risk set |
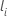 | the last event time at which subject i is in the risk set |
Cox-Snell residuals
 has the following form:
has the following form: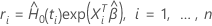
where  is the Breslow's estimator of the baseline cumulative hazard rate:
is the Breslow's estimator of the baseline cumulative hazard rate:

 is a step function with jumps at the observed event times. The size of the jump
at time
is a step function with jumps at the observed event times. The size of the jump
at time  has the following form:
has the following form: 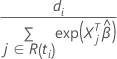

For the Efron approximation, the Cox-Snell residual has the following form:
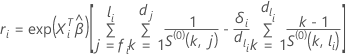
where 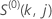 has the following form:
has the following form:
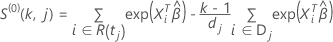
for 
where 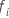 is the first event time at which subject
i is in the risk set and
is the first event time at which subject
i is in the risk set and 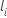 is the last event time at which subject
i is in the risk set.
is the last event time at which subject
i is in the risk set.
Martingale residuals

where 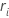 is the Cox-Snell residual and depends on the tie handling method. Additionally,
is the Cox-Snell residual and depends on the tie handling method. Additionally,
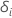 is an indicator for if subject
i is censored, such that
is an indicator for if subject
i is censored, such that 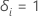 if subject
i experienced the event and
if subject
i experienced the event and 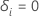 otherwise.
otherwise.
Deviance residuals

where  is the Martingale residual for subject
i.
is the Martingale residual for subject
i.
Schoenfeld residual vector
The Schoenfeld residual vector is a p-component vector. For subject i with event time t the Schoenfeld residual vector has the following form:
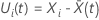
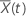 is the weighted average of the covariates over the risk set at time t. The
weighted average has the following form:
is the weighted average of the covariates over the risk set at time t. The
weighted average has the following form: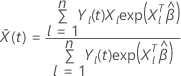
where 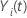 is an indicator variable that has the value 1 if subject
i is at risk at time
t and 0 otherwise, which is equivalent to
is an indicator variable that has the value 1 if subject
i is at risk at time
t and 0 otherwise, which is equivalent to
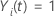 if
if 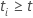 and
and 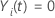 otherwise.
otherwise.
If the subject does not experience the event at time t, the vector contains missing values.
The calculation of the Schoenfeld residual vector depends on the tie handling method. For the Breslow approximation, the Schoenfeld residual vector has the following form:
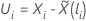
where
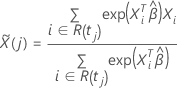
For the Efron approximation, the Schoenfeld residual vector has the following form:
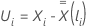
where
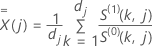
the function 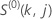 has the same definition as for the Cox-Snell residual:
has the same definition as for the Cox-Snell residual:
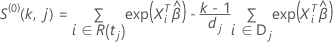
and

for 
Scaled Schoenfeld residual vector
The scaled Schoenfeld residual vector has the following form:

where  is the observed number of uncensored survival times and
is the observed number of uncensored survival times and
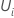 is the Schoenfeld residual vector.
is the Schoenfeld residual vector.
Score residual vector
The calculation of the score residual vector depends on the approximation method for ties in the event times. For the Breslow approximation, the score residual vector has the following form:
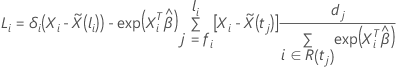
where

For the Efron approximation, the score residual vector has the following form:
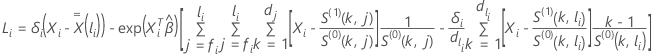
where 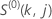 ,
,
 and
and  have the same definitions as for the Schoenfeld residual vector:
have the same definitions as for the Schoenfeld residual vector:
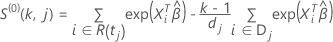

and
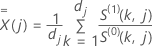
for 
DFBeta
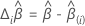

where 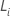 is the score residual vector. For details on the calculation of
is the score residual vector. For details on the calculation of
 ,
go to
Methods and formulas for the coefficients and regression equation for Fit Cox Model with Fixed Predictors only.
,
go to
Methods and formulas for the coefficients and regression equation for Fit Cox Model with Fixed Predictors only.