In This Topic
Step 1: Determine how well the model fits your data
- P-value ≤ α: The model fits the data well
- If the p-value is less than or equal to the significance level, you can conclude that the model fits the data well. You should examine whether any of the terms are statistically significant and also ensure that the model satisfies the proportional hazards assumption.
- P-value > α: There is not enough evidence to conclude that the model fits the data well
- If the p-value is greater than the significance level, you cannot conclude that the model fits the data well. You may want to refit the model with different terms.
Goodness-of-Fit Tests
| Test | DF | Chi-Square | P-Value |
|---|---|---|---|
| Likelihood Ratio | 4 | 18.31 | 0.001 |
| Wald | 4 | 21.15 | 0.000 |
| Score | 4 | 24.78 | 0.000 |
Key Results: P-Value
In these results, the p-values for all 3 tests are below 0.05, so you can conclude that the model fits the data well.
Step 2: Determine whether the association between the response and the term is statistically significant
- P-value ≤ α: The association is statistically significant
- If the p-value is less than or equal to the significance level, you can conclude that there is a statistically significant association between the response variable and the term.
- P-value > α: The association is not statistically significant
- If the p-value is greater than the significance level, you cannot conclude that there is a statistically significant association between the response variable and the term. You may want to refit the model without the term.
- If a categorical factor is significant, you can conclude that the factor has an effect on the time to the event.
- If a continuous predictor is significant, you can conclude that changes in the value of the predictor are associated with changes in the risk that the subject experiences the event.
- If an interaction term is significant, the relationship between a factor and the response depends on the level of the other factors in the term. In this case, you should not interpret the main effects without considering the interaction effect.
- If a polynomial term is significant, you can conclude that the data contain curvature.
Analysis of Variance
| Wald Test | |||
|---|---|---|---|
| Source | DF | Chi-Square | P-Value |
| Age | 1 | 1.78 | 0.182 |
| Stage | 3 | 17.92 | 0.000 |
Key Results: P-Value
In these results, the p-value for stage is significant at an α-level of 0.05. Therefore, you can conclude that the stage of the cancer has a statistically significant effect on the survival of the patient. However, the p-value for age is 0.182, so the effect of age is not significant at an α-level of 0.05.
Step 3: Determine the relative risks of the predictors
- Categorical variable
In the Relative Risks for Categorical Predictors table, Minitab labels two levels of the categorical variable as Level A and Level B. The relative risk describes the occurrence rate of the event for level A relative to level B. For example, in the following results the risk of experiencing the event for patients in stage IV is 5.5 times higher than the risk for patients in Stage I.
- Continuous variable
- In the Relative Risks for Continuous Predictors table, Minitab displays the unit of change and the relative risk. The relative risk describes the change in the hazard rate for every one unit of change in the predictor value. For example, in the following results a patient is 1.02 times more likely to experience the event for each increase of 1 year to their age.
You can use the confidence interval to determine whether the relative risk is statistically significant. Usually, if the confidence interval contains 1, you cannot conclude that the relative risk is statistically significant.
Relative Risks for Continuous Predictors
| Unit of Change | Relative Risk | 95% CI | |
|---|---|---|---|
| Age | 1 | 1.0192 | (0.9911, 1.0481) |
Relative Risks for Categorical Predictors
| Level A | Level B | Relative Risk | 95% CI |
|---|---|---|---|
| Stage | |||
| II | I | 1.1503 | (0.4647, 2.8477) |
| III | I | 1.9010 | (0.9459, 3.8204) |
| IV | I | 5.5068 | (2.4086, 12.5901) |
| III | II | 1.6526 | (0.6819, 4.0049) |
| IV | II | 4.7872 | (1.7825, 12.8566) |
| IV | III | 2.8968 | (1.2952, 6.4788) |
Key Results: Relative Risk, 95% CI
Step 4: Determine whether the model satisfies the proportional hazards assumption
- Tests for Proportional Hazards table
Use the tests to determine whether the model meets the proportional hazards assumption. The null hypothesis is that the model meets the assumption for all the predictors. Usually, a significance level (denoted as α or alpha) of 0.05 works well. A significance level of 0.05 indicates a 5% risk of concluding that the model meets the assumption when it actually does not.
If the p-value is less than or equal to the significance level, you can conclude that the model does not meet the assumption of proportional hazards. If the p-value is greater than the significance level, you cannot conclude that the model does not meet the assumption.
- Arjas plot
Use the Arjas plot to determine whether the model meets the proportional hazards assumption for a categorical predictor. If the curves on the plot differ from the 45 degree line, then the model does not meet the proportional hazards assumption for the predictor.
If the model does not meet the assumption for a variable, try using the variable as a stratification variable instead.
- Andersen plot
Use the Andersen plot to determine whether the model meets the proportional hazards assumption for different strata. Each combination of values of one or more stratification variables defines a stratum. The plot contains a curve for each stratum. If the model meets the assumption, the curves are straight lines through the point where X = 0 and Y = 0. If the baseline hazard rate for a stratum is the same as the baseline hazard rate for the stratum on the x-axis, then the curve follows the 45 degree reference line on the plot.
If the model does not meet the assumption, consider whether to divide the data by the stratification variable for which the model does not meet the proportional hazards assumption. Then perform a separate analysis on each subset of the data. The separate analyses provide different effects for the predictors in each subset.
Tests for Proportional Hazards
| Term | DF | Correlation | Chi-Square | P-Value |
|---|---|---|---|---|
| Age | 1 | 0.1328 | 1.18 | 0.278 |
| Stage | ||||
| II | 1 | -0.0104 | 0.01 | 0.940 |
| III | 1 | -0.2445 | 2.86 | 0.091 |
| IV | 1 | -0.1193 | 0.63 | 0.426 |
| Overall | 4 | — | 4.61 | 0.330 |
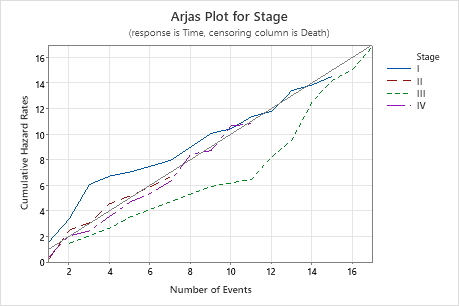
Key Results: P-value, Arjas plot
In these results, the p-values for the test for proportional hazards are all greater than 0.05, so you cannot conclude that the model does not meet the proportional hazards assumption.
The Arjas plot displays the cumulative hazard rates versus the number of events for each level of Stage. In this Arjas plot, the lines generally follow the 45 degree line, so you can conclude that the model meets the proportional hazards assumption for the predictor Stage.
