In This Topic
Intercept and slope specified
When the scale σ (or Weibull shape β), the intercept (β0), and the slope are specified (β1), the standardized intercept is calculated as follows:
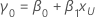
The standardized slope is calculated as follows:
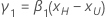
Notation
| Term | Description |
|---|---|
| σ | specified value for the scale |
| β | specified value for the Weibull shape |
| specified value for the intercept | |
| β1 | specified value for the slope |
| γ0 | standardized intercept |
| γ1 | standardized slope |
Percentile and slope specified
When the scale (or Weibull shape), the slope, and a percentile are specified, the standardized slope and intercept are calculated as follows.
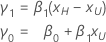
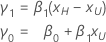
where

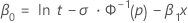

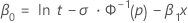
Notation
| Term | Description |
|---|---|
| σ | specified planning value for the scale |
| β | specified planning value for the Weibull shape |
| β0 | intercept |
| β1 | specified planning value of the slope |
| t | specified planning value of a percentile |
| Φ-1(p) | inverse CDF of the chosen distribution |
| p | proportion of failures at stress level x |
| x | stress level |
Percentile and intercept specified
When the scale (or Weibull shape), the intercept, and a percentile are specified, the standardized slope and intercept are calculated as follows:
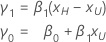
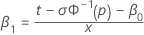
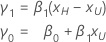
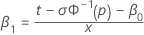
for location-scale models (normal, logistic and smallest extreme value)
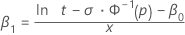
for log-location-scale models (Weibull, exponential, lognormal and loglogistic)
Notation
| Term | Description |
|---|---|
| σ | specified planning value for the scale |
| β | specified planning value for the Weibull shape |
| β0 | specified planning value of the intercept |
| β1 | slope |
| t | specified planning value of a percentile |
| Φ-1(p) | inverse CDF of the chosen distribution |
| p | proportion of failures at stress level x |
| x | stress level |
Two percentiles specified
When the scale (or Weibull shape) and two percentiles are specified, the standardized slope and intercept are calculated as follows.
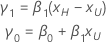
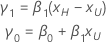
where:
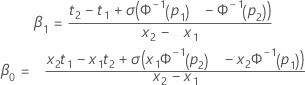
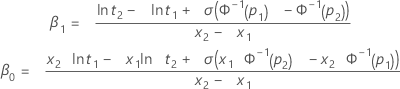
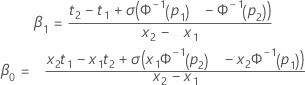
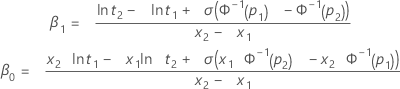
Notation
| Term | Description |
|---|---|
| σ | specified planning value for the scale |
| β | specified planning value for the Weibull shape |
| β0 | intercept |
| β1 | slope |
| t1 | specified planning value for a percentile |
| t2 | specified planning value for a percentile |
| Φ-1(p) | standard inverse cdf of the chosen distribution |
| p1 | proportion of failures at stress level x1 |
| p2 | proportion of failures at stress level x2 |
| x1 | stress level |
| x2 | stress level |
