Linear

Notation
| Term | Description |
|---|---|
| Yp | failure time or log failure time |
| β0 | y-intercept (constant) |
| β1 | regression coefficient |
| σ | reciprocal of the shape parameter (Weibull distribution) or the scale parameter (other distributions) |
| Φ-1(p) | the pth quantile of the standardized life distribution |
Arrhenius

where the value in the numerator (11604.53) is the inverted value of Boltzman's constant and the value in the denominator (273.16) is absolute 0.
Notation
| Term | Description |
|---|---|
| Yp | failure time or log failure time |
| β0 | y-intercept (constant) |
| β1 | regression coefficient |
| σ | reciprocal of the shape parameter (Weibull distribution) or the scale parameter (other distributions) |
| Φ-1(p) | the pth quantile of the standardized life distribution |
Inverse temp

Notation
| Term | Description |
|---|---|
| Yp | failure time or log failure time |
| β0 | y-intercept (constant) |
| β1 | regression coefficient |
| σ | reciprocal of the shape parameter (Weibull distribution) or the scale parameter (other distributions) |
| Φ-1(p) | the pth quantile of the standardized life distribution |
Ln (Power)

Notation
| Term | Description |
|---|---|
| Yp | failure time or log failure time |
| β0 | y-intercept (constant) |
| β1 | regression coefficient |
| σ | reciprocal of the shape parameter (Weibull distribution) or the scale parameter (other distributions) |
| Φ-1(p) | the pth quantile of the standardized life distribution |
Standardized model
The standardized acceleration is calculated as follows:
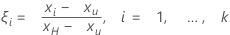
The standardized accelerated life test model is:

Notation
| Term | Description |
|---|---|
| k | number of levels of the accelerating variable (not including the normal use level) |
| Xi | level of the accelerating variable |
| XU | use level |
| XH | highest level of the accelerating variable |
