When to transform a response variable
A transformation might be necessary when the residuals exhibit nonconstant variance or nonnormality.
Transformations might also be useful when the model exhibits significant lack of fit, which is especially important in the analysis of response surface experiments. Suppose you include all significant interactions and quadratic terms in the model, but the lack-of-fit test indicates the need for higher-order terms. A transformation can eliminate the lack of fit.
If the transformation corrects the problem, you can use regression analysis in favor of other, potentially more complicated, analyses. A good book on regression or analysis of designed experiments can provide appropriate guidance about which transformations solve different problems.
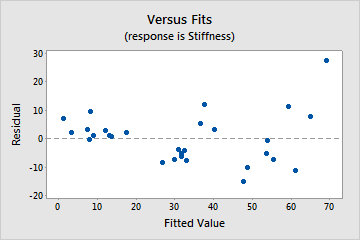
Untransformed data
In this graph, the residuals exhibit nonconstant variance.
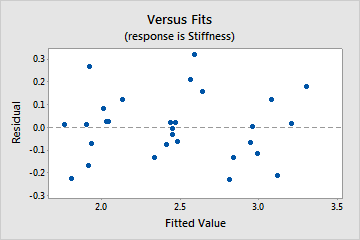
Transformed data
This graph shows the residuals after a variance-stabilizing transformation. The scale of the fitted values (x-axis) changes and the variance becomes constant.
Transform a response variable
You can transform your data using many functions such as square root, logarithm, power, reciprocal or arcsine.
- To apply these transformations directly to your data in the worksheet, use the Minitab Calculator.
- To perform a Box-Cox transformation, start the analysis, then click Options.
- Under Box-Cox transformation, let Minitab determine an optimal lambda or specify the lambda that you want.
