Methods for Stability Study for random batches

Select the method of your choice.

In This Topic

The mixed model and log-likelihood
Box-Cox transformation
Random batch model selection

The mixed model and log-likelihood

The general form of the mixed model

Mixed effect models contain both fixed and random effects. The general form of the mixed effect model is:

y = Xβ + Z₁μ₁ + Z₂μ₂ + ... + Z_cμ_c + ε

Notation

Term	Description
y	the n x 1 vector of response values
X	the n x p design matrix for the fixed effects, p ≤ n
Z_i	the n x m_i design matrix for the i^th random effect in the model
β	a p x 1 vector of unknown parameters
μ_i	an m_i x 1 vector of independent variables from N(0, σ²_i)
ε	an n x 1 vector of independent variables from N(0, σ²_i)
c	the number of random effects in the model

Particular forms of the mixed model

Stability studies fits two models with a random batch factor. The largest model contains time, the random batch factor, and the random interaction between time and batch.

y = Xβ + Z₁μ₁ + Z₂μ₂ + ε

The smaller model contains time and the random batch factor.

y = Xβ + Z₁μ₁ + ε

The general variance-covariance matrix of the response vector, y, is:

V(σ²) = V(σ², σ²₁, ... , σ²_c) = σ²I_n + σ²₁Z₁Z'₁ + ... + σ²_cZ_cZ'_c

where

σ² = (σ², σ²₁, ... , σ²_c)'

σ², σ²₁, ... , σ²_c are called variance components.

By factoring from the variance, you can find a representation of H(θ), which is in the computation of the log-likelihood of mixed models.

V(σ²) = σ²H(θ) = σ²[I_n + θ₁Z₁Z'₁ + ... + θ_cZ_cZ'_c]

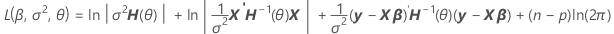
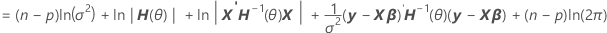
When batch is a random factor, the unknown parameter estimates come from minimizing twice the negative of the restricted log-likelihood function. The minimization is equivalent to maximizing the restricted log-likelihood function. The function to minimize is:

Notation

Term	Description
n	the number of observations
p	the number of parameters in β, 2 for stability studies
σ²	the error variance component
X	the design matrix ––for the fixed terms, the constant and time
H(θ)	I_n + θ₁Z₁Z'₁ + ... + θ_cZ_cZ'_c
I_n	the identity matrix with n rows and columns
θ_i	the ratio of the variance of the i^th random term over the error variance
Z_i	the n x m_i matrix of known codings for the i^th random effect in the model
m_i	the number of levels for the i^th random effect
c	the number of random effects in the model
\|H(θ)\|	the determinant of H(θ)
X'	the transpose of X
H^-1(θ)	the inverse of H(θ)

Box-Cox transformation

Box-Cox transformation selects lambda values, as shown below, which minimize the residual sum of squares. The resulting transformation is Y ^λ when λ ≠ 0 and ln(Y) when λ = 0. When λ < 0, Minitab also multiplies the transformed response by −1 to maintain the order from the untransformed response.

Minitab searches for an optimal value between −2 and 2. Values that fall outside of this interval might not result in a better fit.

Here are some common transformations where Y′ is the transform of the data Y:

Lambda (λ) value	Transformation
λ = 2	Y′ = Y ²
λ = 0.5	Y′ =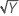
λ = 0	Y′ = ln(Y )
λ = −0.5
λ = −1	Y′ = −1 / Y

Random batch model selection

The model selection determines whether the shelf life depends on batch and whether the effect of time depends on the batch. Minitab considers the following three models in sequence:

Time + Batch + Batch*Time (unequal slopes and intercepts for batches)
Time + Batch (equal slopes and unequal intercepts for batches)
Time (equal slopes and intercepts for batches)

If the Batch*Time interaction is significant, the analysis fits the first model. If the interaction is not significant but the Batch term is significant in the second model, the analysis fits the second model. Otherwise, the analysis fits the third model.

The test for whether to pool batches is slightly different from the test to include batch, although both depend on the chi-square distribution. The formulas for the test statistics and p-values are as follow.

Test between model 1 and model 2

difference = −2L₂ − (−2L₁)

p = 0.5 * Prob(χ²₁ > difference) + 0.5 * Prob(χ²₂ > difference)

Test between model 2 and model 3

difference = −2L₃ − (−2L₂)

p = 0.5 * Prob(χ²₁ > difference)

Notation

Term	Description
L_a	the log-likelihood for model a
p	the p-value for the test
Prob(χ²₁> difference)	the probability that a random variable from a chi-square distribution with 1 degree of freedom is greater than the difference
Prob(χ²₂> difference)	the probability that a random variable from a chi-square distribution with 2 degrees of freedom is greater than the difference

References

Searle, S.R. Casella, G. and McCuloch, C.E. (1992). Variance Components
West, B.T., Welch, K.B. and Galecki, A.T. (2007). Linear Mixed Models: A Practical Guide Using Statistical Software.
Chow, S. (2007). Statistical Design and Analysis of Stability Studies.