In This Topic
Box-Cox transformation
Box-Cox transformation selects lambda values, as shown below, which minimize the residual sum of squares. The resulting transformation is Y λ when λ ≠ 0 and ln(Y) when λ = 0. When λ < 0, Minitab also multiplies the transformed response by −1 to maintain the order from the untransformed response.
Minitab searches for an optimal value between −2 and 2. Values that fall outside of this interval might not result in a better fit.
Here are some common transformations where Y′ is the transform of the data Y:
| Lambda (λ) value | Transformation |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0.5 | Y′ = 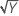 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0.5 |  |
| λ = −1 | Y′ = −1 / Y |
Fixed batch model selection
- Time + Batch + Batch*Time (unequal slopes and intercepts for batches)
- Time + Batch (equal slopes and unequal intercepts for batches)
- Time (equal slopes and intercepts for batches)
If the Batch*Time interaction is significant, the analysis fits the first model. If the interaction is not significant but the Batch term is significant in the second model, the analysis fits the second model. Otherwise, the analysis fits the third model.
The test statistic is:
- Numerator degrees of freedom = degrees of freedom for the term
- Denominator degrees of freedom = degrees of freedom for error

Notation
| Term | Description |
|---|---|
| MS | the mean square |
| MSE | the mean square for error |
| F(x) | the cumulative distribution function of the given F-distribution evaluated at x |
References
1. Chow, S. (2007). Statistical Design and Analysis of Stability Studies.
2. U.S. Department of Health and Human Services, Food and Drug Administration, (2004). Guidance for Industry, Q1E Evaluation of Stability Data.
