In This Topic
Histogram of residuals
The histogram of the residuals shows the distribution of the residuals for all observations.
Interpretation
| Pattern | What the pattern may indicate |
|---|---|
| A long tail in one direction | Skewness |
| A bar that is far away from the other bars | An outlier |
Because the appearance of a histogram depends on the number of intervals used to group the data, don't use a histogram to assess the normality of the residuals. Instead, use a normal probability plot.
A histogram is most effective when you have approximately 20 or more data points. If the sample is too small, then each bar on the histogram does not contain enough data points to reliably show skewness or outliers.
Normal probability plot of residuals
The normal probability plot of the residuals displays the residuals versus their expected values when the distribution is normal.
Note
If the batch factor is random, use the conditional residuals to evaluate normality.
Interpretation
Use the normal probability plot of the residuals to verify the assumption that the residuals are normally distributed. The normal probability plot of the residuals should approximately follow a straight line.
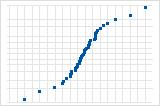
S-curve implies a distribution with long tails.
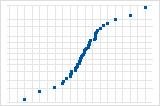
Inverted S-curve implies a distribution with short tails.
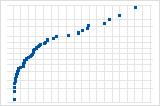
Downward curve implies a right-skewed distribution.
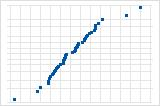
A few points lying away from the line implies a distribution with outliers.
If you see a nonnormal pattern, use the other residual plots to check for other problems with the model, such as non-constant variance or a time order effect. If the residuals do not follow a normal distribution and the data have fewer than 15 observations, then confidence intervals for predictions, confidence intervals for coefficients, and p-values for coefficients can be inaccurate.
Residuals versus fits

Plot with outlier
One of the points is much larger than all of the other points. Therefore, the point is an outlier. If there are too many outliers, the model may not be acceptable. You should try to identify the cause of any outlier. Correct any data entry or measurement errors. Consider removing data values that are associated with abnormal, one-time events (special causes). Then, repeat the analysis.
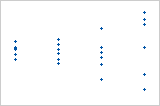
Plot with nonconstant variance
The variance of the residuals increases with the fitted values. Notice that, as the value of the fits increases, the scatter among the residuals widens. This pattern indicates that the variances of the residuals are unequal (nonconstant).
If you identify any patterns or outliers in your residual versus fits plot, consider the following solutions:
| Issue | Possible solution |
|---|---|
| Nonconstant variance | Consider using a Box-Cox transformation. For more information, go to Perform Box-Cox transformation for Stability Study. |
| An outlier or influential point |
|
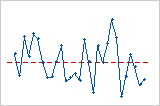
Residuals versus order
The residuals versus order plot displays the residuals in the order that the data were collected.
Interpretation
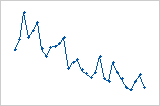
Trend
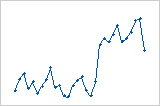
Shift
Cycle
Residuals versus the variables
The residual versus variables plot displays the residuals versus another variable. The variable could already be included in your model. Or, the variable may not be in the model, but you suspect it affects the response.
Interpretation
If you see a non-random pattern in the residuals, it indicates that the variable affects the response in a systematic way. Consider including this variable in an analysis.
