In This Topic
Regression equation
Use the regression equation to describe the relationship between the response and the terms in the model. The regression equation is an algebraic representation of the regression line. The regression equation for the linear model takes the following form: Y= b0 + b1x1. In the regression equation, Y is the response variable, b0 is the constant or intercept, b1 is the estimated coefficient for the linear term (also known as the slope of the line), and x1 is the value of the term.
The regression equation with more than one term takes the following form:
y = b0 + b1X1 + b2X2 + ... + bkXk
- y is the response variable
- b0 is the constant
- b1, b2, ..., bk are the coefficients
- X1, X2, ..., Xk are the values of the term
If the model contains both continuous and categorical variables, the regression equation table can display an equation for each combination of levels for the categorical variables. To use these equations for prediction, you must choose the correct equation, based on the values of the categorical variables, and then enter the values of the continuous variables.
Variable settings
The model uses the settings for the variables to calculate the predictions. If the variable settings are unusual compared to the data that Minitab used to estimate the model, then Minitab displays a warning below the prediction.
Fit
Fitted values are also called fits or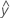 
. The fitted values are point estimates of the mean response for given values of the predictors. The values of the predictors are also called x-values.
Interpretation
Fitted values are calculated by entering the specific x-values for each observation in the data set into the model equation.
For example, if the equation is y = 5 + 10x, the fitted value for the x-value, 2, is 25 (25 = 5 + 10(2)).
Minitab notes predictions with unusual predictor values compared to the values in the data. Only further testing with older samples can confirm that your shelf life estimate is accurate.
SE Fit
The standard error of the fit (SE fit) estimates the variation in the estimated mean response for the specified variable settings. The calculation of the confidence interval for the mean response uses the standard error of the fit. Standard errors are always non-negative.
Interpretation
Use the standard error of the fit to measure the precision of the estimate of the mean response. The smaller the standard error, the more precise the predicted mean response. For example, an analyst develops a model to predict delivery time. For one set of variable settings, the model predicts a mean delivery time of 3.80 days. The standard error of the fit for these settings is 0.08 days. For a second set of variable settings, the model produces the same mean delivery time with a standard error of the fit of 0.02 days. The analyst can be more confident that the mean delivery time for the second set of variable settings is close to 3.80 days.
With the fitted value, you can use the standard error of the fit to create a confidence interval for the mean response. For example, depending on the number of degrees of freedom, a 95% confidence interval extends approximately two standard errors above and below the predicted mean. For the delivery times, the 95% confidence interval for the predicted mean of 3.80 days when the standard error is 0.08 is (3.64, 3.96) days. You can be 95% confident that the population mean is within this range. When the standard error is 0.02, the 95% confidence interval is (3.76, 3.84) days. The confidence interval for the second set of variable settings is narrower because the standard error is smaller.
Confidence interval for fit (95% CI)
These confidence intervals (CI) are ranges of values that are likely to contain the mean response for the population that has the observed values of the predictors or factors in the model.
Because samples are random, two samples from a population are unlikely to yield identical confidence intervals. But, if you sample many times, a certain percentage of the resulting confidence intervals contain the unknown population parameter. The percentage of these confidence intervals that contain the parameter is the confidence level of the interval.
- Point estimate
- The point estimate is the estimate of the parameter that is calculated from the sample data. The confidence interval is centered around this value.
- Margin of error
- The margin of error defines the width of the confidence interval and is determined by the observed variability in the sample, the sample size, and the confidence level. To calculate the upper limit of the confidence interval, the error margin is added to the point estimate. To calculate the lower limit of the confidence interval, the error margin is subtracted from the point estimate.
Interpretation
Use the confidence interval to assess the estimate of the fitted value for the observed values of the variables.
For example, with a 95% confidence level, you can be 95% confident that the confidence interval contains the population mean for the specified values of the predictor variables or factors in the model. The confidence interval helps you assess the practical significance of your results. Use your specialized knowledge to determine whether the confidence interval includes values that have practical significance for your situation. A wide confidence interval indicates that you can be less confident about the mean of future values. If the interval is too wide to be useful, consider increasing your sample size.
95% PI
The prediction interval is a range that is likely to contain a single future response for a selected combination of variable settings. The prediction interval is always wider than the corresponding confidence interval.
Interpretation
For example, a quality engineer determined that the shelf life of a new medication is 54.79 months. The shelf life for this analysis is defined as the time at which the engineer can no longer be 95% confident that the concentration of the worst batch is 90% of the intended concentration. The engineer wants to predict the mean concentration for the worst batch at 54.79 months.
In these results, the prediction for the mean response is about 91.36%. However, the engineer also wants to estimate the range of values for a single pill from Batch 2. The prediction interval indicates that you can be 95% confidence that the predicted concentration for a single pill from Batch 2 at 54.79 months is between approximately 89.3217% and 93.4001%.
Settings
| Variable | Setting |
|---|---|
| Month | 54.79 |
| Batch | 2 |
Prediction
| Fit | SE Fit | 95% CI | 95% PI | |
|---|---|---|---|---|
| 91.3609 | 0.801867 | (89.7233, 92.9986) | (89.3217, 93.4001) | XX |
