Fits
Fitted values are also called fits or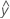 
. The fitted values are point estimates of the mean response for given values of the predictors. The values of the predictors are also called x-values.
Interpretation
Fitted values are calculated by entering the specific x-values for each observation in the data set into the model equation.
For example, if the equation is y = 5 + 10x, the fitted value for the x-value, 2, is 25 (25 = 5 + 10(2)).
SE Fit
The standard error of the fit (SE fit) estimates the variation in the estimated mean response for the specified variable settings. The calculation of the confidence interval for the mean response uses the standard error of the fit. Standard errors are always non-negative.
Interpretation
Use the standard error of the fit to measure the precision of the estimate of the mean response. The smaller the standard error, the more precise the predicted mean response. For example, an analyst develops a model to predict delivery time. For one set of variable settings, the model predicts a mean delivery time of 3.80 days. The standard error of the fit for these settings is 0.08 days. For a second set of variable settings, the model produces the same mean delivery time with a standard error of the fit of 0.02 days. The analyst can be more confident that the mean delivery time for the second set of variable settings is close to 3.80 days.
With the fitted value, you can use the standard error of the fit to create a confidence interval for the mean response. For example, depending on the number of degrees of freedom, a 95% confidence interval extends approximately two standard errors above and below the predicted mean. For the delivery times, the 95% confidence interval for the predicted mean of 3.80 days when the standard error is 0.08 is (3.64, 3.96) days. You can be 95% confident that the population mean is within this range. When the standard error is 0.02, the 95% confidence interval is (3.76, 3.84) days. The confidence interval for the second set of variable settings is narrower because the standard error is smaller.
95% CI
The confidence interval for the fit provides a range of likely values for the mean response given the specified settings of the predictors.
Interpretation
Use the confidence interval to assess the estimate of the fitted value for the observed values of the variables.
For example, with a 95% confidence level, you can be 95% confident that the confidence interval contains the population mean for the specified values of the variables in the model. The confidence interval helps you assess the practical significance of your results. Use your specialized knowledge to determine whether the confidence interval includes values that have practical significance for your situation. A wide confidence interval indicates that you can be less confident about the mean of future values. If the interval is too wide to be useful, consider increasing your sample size.
95% PI
The prediction interval is a range that is likely to contain a single future response for a value of the predictor variable.
Interpretation
With the 95% prediction interval, you can be 95% confident that new observations will fall withing the interval. (Note, however, that this is only true for values that are included within the range of the data in the analysis.) The interval is defined by lower and upper limits, which are calculated from the confidence level and the standard error of the prediction. The prediction interval is always wider than the confidence interval because of the added uncertainty involved in predicting a single response versus the mean response.
Test R-sq
The test R2 represents the proportion of variation in the responses that is explained by the original model using predictor values from the test data.
The test data set must include the same number of predictors as the original data set. The test R2 can only be calculated if the test data includes response data for each observation. The test R2 is calculated in the same way as R2.
Interpretation
Test R2 identifies how well the PLS regression model predicts your test data. Higher test R2 values indicate the model has greater predictive ability.
Often, PLS regression is performed in two steps. The first step, sometimes called training, involves calculating a PLS regression model for a sample data set (also called a training data set). The second step involves validating this model with a different set of data, often called a test data set. Some test data sets include response values, others do not. If the test data set does include response values, then Minitab can calculate a test R2.
If you use cross-validation, compare the test R2 to the predicted R2. Ideally, these values should be similar. A test R2 that is significantly smaller than the predicted R2 indicates that cross-validation is overly optimistic about the model's predictive ability or that the two data samples are from different populations.
