Minitab®  Support

Graphs for Partial Least Squares Regression

Learn more about Minitab
Find definitions and interpretation guidance for every graph available with PLS.

In This Topic

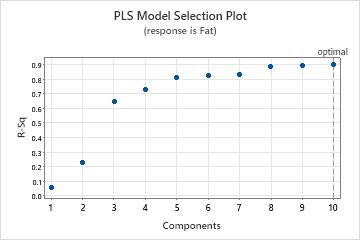
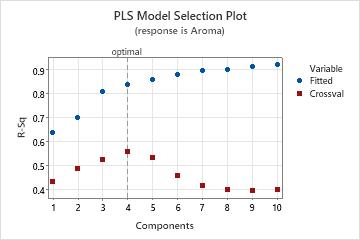
Model selection plot

The model selection plot is a scatterplot of the R2 and predicted R2 values as a function of the number of components that are fit or cross-validated. It is a graphical display of the Model Selection and Validation table. If you do not use cross-validation, the predicted R2 values do not appear on your plot. Minitab provides one model selection plot per response.

Interpretation

Use this plot to compare the modeling and predicting power of different models to determine the appropriate number of components to retain in your model. The vertical line on the plot indicates the number of components Minitab selected for the PLS model.

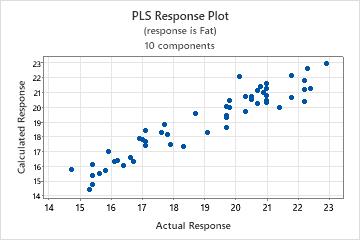
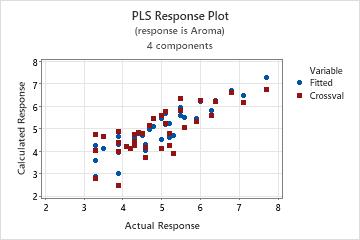
In this plot, cross-validation was not used to select the components. Minitab fits the default 10 components and displays the R2 values for each model on the plot.
In this plot, cross-validation was used to select the model. The blue circles represent the R2 values and the red squares represent the predicted R2 values for each model. Minitab selected the model with 4 components because it had the highest predicted R2.

Response plot

The response plot is a scatterplot of the fitted values versus the actual responses. If you perform cross-validation, the plot also includes the fitted values versus the cross-validated fitted values. Minitab provides one response plot per response.

Interpretation

Use this plot to determine how well your model fits and predicts each observation. When examining this plot, look for the following things:
  • A nonlinear pattern in the points, which indicates the model may not fit or predict data well.
  • If you perform cross-validation, large differences in the fitted and the cross-validated values, which indicate a leverage point.

A model with excellent predictive capability usually has a slope of 1 and intersects the y-axis at 0.

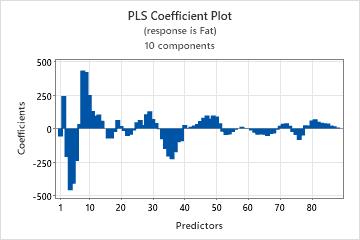
In the first plot, the points follow a linear pattern, indicating that the model fits the data well and accurately predicts the response. In the second plot, cross-validation was used so both the fitted and cross-validated fitted values appear on the plot. The plot does not reveal differences between the fitted and cross-validated fitted responses.

Coefficient plot

The coefficient plot is a projected scatterplot showing the unstandardized coefficients for each predictor. Minitab provides one coefficient plot per response.

Interpretation

Use the coefficient plot, along with the output of regression coefficients to compare the sign and magnitude of the coefficients for each predictor. The plot makes it easier to quickly identify predictors that are more or less important in the model.

Because the plot displays unstandardized coefficients, you can only make comparisons among the magnitude of the relationships between predictors and the response if your predictors are on the same scale (for example, spectral data). Otherwise, use the standardized coefficient plot or use the loading plot to compare the weights of predictors used to calculate the components.

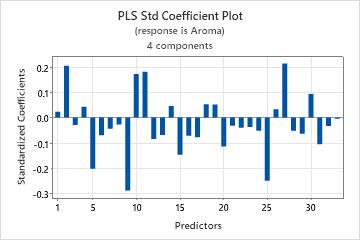
In this plot, the predictors (spectral data) are on the same scale. The plot indicates that wavelengths 1 - 40 have the greatest influence on the responses.

Std coefficient plot

The coefficient plot is a projected scatterplot showing the standardized coefficients for each predictor. Minitab provides one standardized coefficient plot per response.

Interpretation

Use this plot, along with the output of regression coefficients to compare the sign and magnitude of the coefficients for each predictor. The plot makes it easier to quickly identify predictors that are more or less important in the model.

Because the plot displays standardized coefficients, you can make comparisons among the magnitude of the relationships between predictors and the response even if your predictors are not on the same scale.

If your predictors are on the same scale, the pattern of coefficients in standardized and unstandardized plots look similar. These plots may not look identical, though, because the predictors are highly correlated, causing the coefficients to be unstable and because of differences between sample standard deviations and population standard deviations.

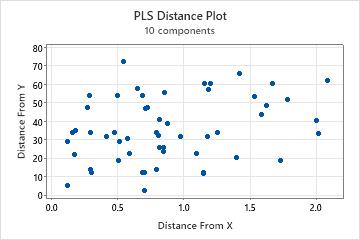
In this plot, the elements with the longest bars have the largest standardized coefficients and the biggest impact on aroma. The elements above the center line are positively related to aroma, while the elements below the center line are negatively related.

Distance plot

The distance plot is a scatterplot of each observation's distance from the x- and y-model. Distances from the y-model measure how well an observation is fitted in the y-space. Distances from the x-model measure how well an observation is fitted in the x-space.

Interpretation

When examining this plot, look for points with distances greater than other points on the x- or y-axis. Observations with greater distances from the y-model may be outliers and observations with greater distances from the x-model may be leverage points.

In this plot, none of the points look like extreme outliers or leverage points.

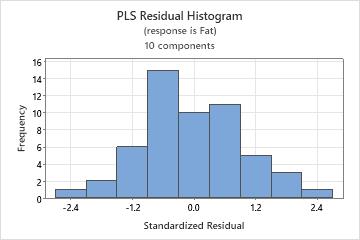
Histogram of residuals

The histogram of the standardized residuals shows the distribution of the standardized residuals for all observations.

Interpretation

Use the histogram of the residuals to determine whether the data are skewed or include outliers. The patterns in the following table may indicate that the model does not meet the model assumptions.
Pattern What the pattern may indicate
A long tail in one direction Skewness
A bar that is far away from the other bars An outlier

Because the appearance of a histogram depends on the number of intervals used to group the data, don't use a histogram to assess the normality of the residuals. Instead, use a normal probability plot. A histogram is most effective when you have approximately 20 or more data points. If the sample is too small, then each bar on the histogram does not contain enough data points to reliably show skewness or outliers.

This histogram of the standardized residuals reveals a bell-shaped, symmetric pattern, indicating the residuals are not skewed and there are no outliers.

Normal probability plot of residuals

The normal probability plot of the residuals displays the standardized residuals versus their expected values when the distribution is normal.

Interpretation

Use the normal probability plot of the residuals to verify the assumption that the residuals are normally distributed. The normal probability plot of the residuals should approximately follow a straight line.

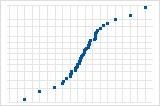
The following patterns violate the assumption that the residuals are normally distributed.

S-curve implies a distribution with long tails.

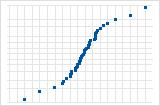
Inverted S-curve implies a distribution with short tails.

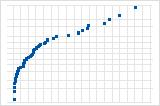
Downward curve implies a right-skewed distribution.

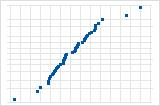
A few points lying away from the line implies a distribution with outliers.

If you see a nonnormal pattern, use the other residual plots to check for other problems with the model, such as missing terms or a time order effect. If the residuals do not follow a normal distribution, the confidence intervals and p-values can be inaccurate.

Residuals versus fits

The residuals versus fits graph plots the standardized residuals on the y-axis and the fitted values on the x-axis.

Interpretation

Use the residuals versus fits plot to verify the assumption that the residuals are randomly distributed and have constant variance. Ideally, the points should fall randomly on both sides of 0, with no recognizable patterns in the points.

The patterns in the following table may indicate that the model does not meet the model assumptions.
Pattern What the pattern may indicate
Fanning or uneven spreading of residuals across fitted values Nonconstant variance
Curvilinear A missing higher-order term
A point that is far away from zero An outlier
A point that is far away from the other points in the x-direction An influential point
The following graphs show an outlier and a violation of the assumption that the variance of the residuals is constant.
Plot with outlier

One of the points is much larger than all of the other points. Therefore, the point is an outlier. If there are too many outliers, the model may not be acceptable. You should try to identify the cause of any outlier. Correct any data entry or measurement errors. Consider removing data values that are associated with abnormal, one-time events (special causes). Then, repeat the analysis.

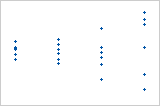
Plot with nonconstant variance

The variance of the residuals increases with the fitted values. Notice that, as the value of the fits increases, the scatter among the residuals widens. This pattern indicates that the variances of the residuals are unequal (nonconstant).

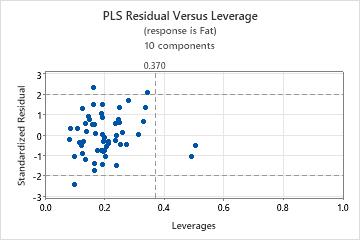
Residual versus leverage plot

The residual versus leverage plot is a scatterplot of the standardized residuals versus the leverage of each observations.

Interpretation

Use the residuals versus leverage plot to identify outliers and leverage points.
  • Outliers: Observations with standardized residuals greater than +/- 2, which lie outside the horizontal reference lines on the plot.
  • Leverage points: Observations with leverage values greater than 2m / n, where m = the number of components and n = the number of observations, which are considered extreme. They have x-scores far from zero and are to the right of the vertical reference line, which is located at the value 2m / n on the x-axis. If 2m / n is greater than one, the reference line doesn't appear on your plot because leverage values are always between 0 and 1.
In this plot, the samples 41 and 42 are leverage points, indicated by their position to the right of the vertical line. Soybean samples 27, 18, and 39 are outliers, indicated by their position above and below the horizontal reference lines. Sample 39 is also an outlier on the residual versus fits plot.

Residuals versus order

The residuals versus order plot displays the standardized residuals in the order that the data were collected.

Interpretation

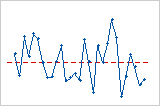
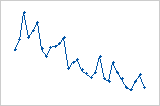
Use the residuals versus order plot to verify the assumption that the residuals are independent from one another. Independent residuals show no trends or patterns when displayed in time order. Patterns in the points may indicate that residuals near each other may be correlated, and thus, not independent. Ideally, the residuals on the plot should fall randomly around the center line:
If you see a pattern, investigate the cause. The following types of patterns may indicate that the residuals are dependent.
Trend
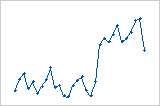
Shift
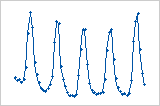
Cycle

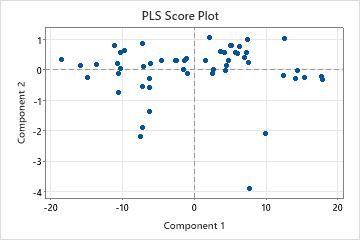
Score plot

The score plot is a scatterplot of the x-scores from the first and second components in the model.

Interpretation

If the first two components explain most of the variance in the predictors, then the configuration of the points on this plot closely reflects the original multidimensional configuration of your data. To check how much variance in the predictors the model explains, examine the x-variance values in the Model Selection and Validation table. If the x-variance value is high, then the model explains significance variance in the predictors.

When examining this plot, look for the following things:
  • Leverage points: Points that lie far from the majority of points on the plot may be leverage points and could have a significant effect on the results.
  • Clusters: Points that group together may indicate two or more separate distributions in your data, which may be described better by different models.
In this plot, brushing the score plot reveals that soybean samples 36, 38, 40, 41, and 42 in the bottom quadrants may have high leverage values. Several of these samples have appeared as outliers or leverage points on other plots. Because the first two components describe 99% of the variance in the predictors, this plot adequately represents the data.
Note

If your model contains more than 2 components, you may want to plot the x-scores of other components using a Scatterplot. To do this, store the x-score matrix and then copy the matrix into columns using Data > Copy > Matrix to Columns. If your model has only one component, this plot does not appear in your output.

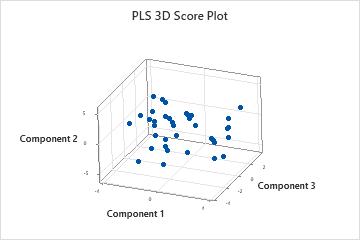
3D score plot

The 3D score plot is a three-dimensional scatterplot of the x-scores from the first, second, and third components in the model. If the first three components explain most of the variance in the predictors, then the configuration of the points on this plot closely reflects the original multidimensional configuration of your data. To check how much variance the model explains, examine the x-variance values in the Model Selection and Validation table. If the x-variance value is high, then the model explains significance variance in the predictors.

Interpretation

When examining the 3D score plot, look for the following things:
  • Leverage points: Points that lie far from the majority of points on the plot may be leverage points and could have a significant effect on the results.
  • Clusters: Points that group together may indicate two or more separate distributions in your data, which may be described better by different models.

You should also use the 3D graph tools, which allow you to rotate the plot so you can view it from different perspectives. This will give you a more complete picture of your data and allow you to more accurately identify leverage points and clusters of points.

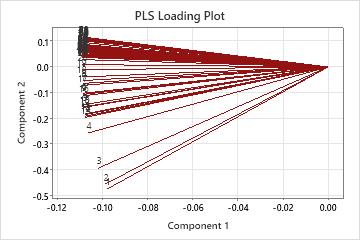
By rotating this 3D score plot, it appears that soybean sample 42 may be a leverage point because of its extreme score for the second component. Sample 42 was identified as a potential leverage point on other plots.

Loading plot

The loading plot is a scatterplot of the predictors projected onto the first and second components in the model. It shows the x-loadings for the second component plotted against the x-loadings of the first component. Each point, representing a predictor, is connected to (0,0) on the plot.

Interpretation

The loading plot shows how important the predictors are to the first two components and is particularly useful when your predictors are on different scales. If the components explain most of the x-variance, which is shown in the Model Selection and Validation table, then the loading plot indicates how important the predictors are in the x-space. When considering the importance of the predictors in the entire model, you must also consider how much variance the components explain in the responses. To check this, examine the R2 and predicted R2 values in the Model Selection and Validation table.

When examining this plot, look for the following things:
  • Angles between the lines, which represent the correlation between the predictors. Smaller angles indicate predictors are highly correlated.
  • Predictors with longer lines, which have greater loadings in the first or second components and are more important in the model.
This loading plot shows that the predictors are highly correlated, because the angles between the lines are small. The lines are almost the same length, indicating the predictors are equally important. On the first component, the predictors have similar negative loadings, indicating they are equally important. On the second component, the first three predictors have larger absolute loadings than the rest.
Note

If your model contains more than 2 components, you may want to plot the x-loadings of other components using a Scatterplot. To do this, store the x-loading matrix and then copy the matrix into columns using Data > Copy > Matrix to Columns.

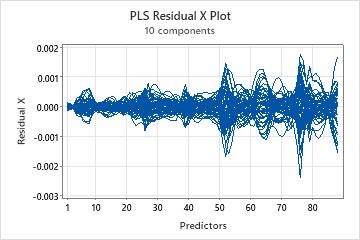
Residual X plot

The residual X plot is a line plot of the x-residuals versus the predictors. Each line represents an observation and has as many points as it has predictors.

Interpretation

Use the x-residual matrix plot to identify observations or predictors that the model describes poorly. This plot is most useful with predictors that are on the same scale.

Ideally, the lines on the plot should be close together and near zero.
  • When the lines are spaced apart at the same point on the x-axis, the model poorly describes the predictor at that point.
  • When a line on the plot deviates from the other lines, the model poorly describes the observation represented by that line.

Use the x-residual matrix plot to examine general patterns in the residuals and identify areas where problems exist. Then, examine the x-residuals displayed in the output to determine which observations and predictors the model describes poorly.

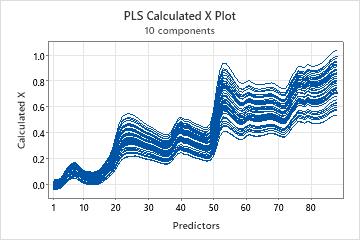
This residual X plot shows that the residuals are close to zero, which indicates that the model describes most of the variance in the predictors. With such small x-residual values, you cannot detect observations or predictors that the model does not describe well.

Calculated X plot

The calculated X plot is a line plot of the x-calculated values versus the predictors. Each line represents an observation and has as many points as it has predictors.

Interpretation

Use this plot to identify observations or predictors that the model describes poorly. This plot is most useful with predictors that are on the same scale.

The calculated X plot complements the x-residual plot. The sum of both plots results in a plot of the original predictor values. A predictor with x-calculated values that are much smaller or larger than the original x-values is not well described by the model.

In this plot, most of the x-calculated values are very close to the original predictor values, indicating that the model describes most of the variance in the predictors.
Copyright © 2024 Minitab, LLC. All rights Reserved.