Methods in Nonlinear Regression

The expectation function for observation n is denoted by:

Minitab considers the expectation function for all N observations as a vector-valued function of the parameters, as:

which is an N X 1 vector with elements .

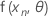
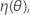
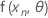The Jacobian of η is a N X P matrix with elements that are equal to the partial derivatives of the expectation function with respect to the parameters:

Let Vⁱ = V(θⁱ) be the Jacobian evaluated at θⁱ, the parameter estimate after iteration i.

Then a linear approximation for η is:

which forms the basis for the Gauss-Newton method and for approximate inferences.

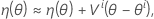
Let θ* denote the least-squares estimate.

By default, Minitab uses the Gauss-Newton method to determine the least squares estimation. The method uses a linear approximation to the expectation function to iteratively improve an initial guess θ⁰ for θ, and then the method keeps improving the estimates until the relative offset falls below the prescribed tolerance¹. That is, Minitab expands the expectation function f(x_n,θ) in a first order Taylor series about θ⁰ as:

where

with p = 1, 2,..., p

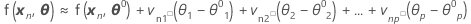
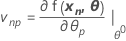
Including all N cases

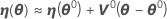
where V⁰ is the NxP derivative matrix with elements {v_np}. This is equivalent to approximating the residuals, z(θ) = y - η(θ), by:

where

and

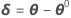
Minitab calculates the Gauss increment δ⁰to minimize the approximate residual sum of squares 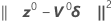, using:

and so: .

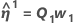
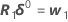The point

should now be closer to y than η(θ⁰), and Minitab uses the value θ¹ = θ⁰ + δ⁰ to perform another iteration by calculating new residuals z¹ = y - η(θ¹), a new derivative matrix V¹, and a new increment. Minitab repeats this process until convergence, which is when the increment is so small that there is no useful change in the elements of the parameter vector.

Sometimes the Gauss-Newton increment produces an increase in the sum of squares. When this occurs, the linear approximation is still a close approximation to the actual surface for a sufficiently small region around η(θ⁰). To reduce the sum of squares, Minitab introduces a step factor λ, and calculates:

Minitab starts with λ = 1 and divides it in half until S(θ¹) < S( θ⁰).

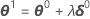
1. Bates and Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.

When the columns in your gradient matrix V have collinearity, it can become singular, causing erratic behavior of Gauss-Newton iterations. To cope with the singularity, Minitab can modify the Gauss-Newton increment to the Levenberg compromise:

or the Marquardt compromise:

where k is a conditioning factor and D is a diagonal matrix with entries that are equal to the diagonal elements of V^TV. The direction of δ(k) is intermediate between the direction of the Gauss-Newton increment (k → 0) and the direction of steepest descent:

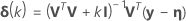
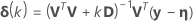
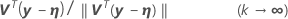.¹

1. Bates and Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.

By default, Minitab declares convergence when the relative offset is less than 1.0e-5. This assures that any inferences are not affected materially by the fact that the current parameter vector is less than 0.001% of the radius of the confidence region disk from the least squares point.¹

1. Bates and Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.