In This Topic
Forward information criteria procedure
- The procedure does not find an improvement in the criterion for 8 consecutive steps.
- The procedure fits the full model.
- The procedure fits a model that leaves 1 degree of freedom for error.
Forward selection procedure
A method for determining which terms to retain in a model. Forward selection adds variables to the model using the same method as the stepwise procedure. Once added, a variable is never removed. The default forward selection procedure ends when none of the candidate variables have a p-value smaller than the value specified in Alpha to enter.
Backward elimination procedure
A method for determining which variables to retain in a model. Backward elimination starts with the model that contains all the terms and then removes terms, one at a time, using the same method as the stepwise procedure. No variable can re-enter the model. The default backward elimination procedure ends when none of the variables included in the model have a p-value greater than the value specified in Alpha to remove. Backward elimination does not proceed if the initial model uses all of the degrees of freedom.
Stepwise method
Performs variable selection by adding or deleting predictors from the existing model based on the F-test. Stepwise is a combination of forward selection and backward elimination procedures. Stepwise selection does not proceed if the initial model uses all of the degrees of freedom.
Variables to remove
Minitab calculates an F-statistic and p-value for each variable in the model. If the model contains j variables, then F for any variable, xr , is this formula:
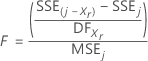
Notation
| Term | Description |
|---|---|
| SSE(j – Xr ) | SS Error for the model that does not contain xr |
| SSE j | SS Error for the model that contains xr |
| MSE j | MS Error for the model that contains xr |
If the p-value for any variable is greater than the value specified in Alpha to remove, then Minitab removes the variable with the largest p-value from the model, calculates the regression equation, displays the results, and initiates the next step.
Variables to add
If Minitab cannot remove a variable, the procedure attempts to add a variable. Minitab calculates an F-statistic and p-value for each variable that is not in the model. If the model contains j variables, then F for any variable, xa, is this formula:
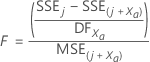
Notation
| Term | Description |
|---|---|
| SSE j | SS Error before xa is added to the model |
| SSE(j + Xa ) | SS Error after xa is added to the model |
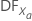 | Degrees of freedom for variable Xa |
| MSE(j + Xa ) | MS Error after xa is added to the model |
If the p-value corresponding to the F-statistic for any variable is smaller than the value specified in Alpha to enter, Minitab adds the variable with the smallest p-value to the model, calculates the regression equation, displays the results, then goes to a new step. When no more variables can be entered into or removed from the model, the stepwise procedure ends.
Forward selection with a test data set
When you use a test data set, the procedure is similar to forward selection. At each step, Minitab adds the term with the smallest p-value to the model. At the end of each step, Minitab calculates the test deviance R2 value. At the end of the forward selection procedure, the model with the greatest test deviance R2 value is the final model.
- The procedure does not find an improvement in the criterion for 8 consecutive steps.
- The procedure fits the full model.
- The procedure fits a model that leaves 1 degree of freedom for error.
