In This Topic
Computational routine
In best subsets regression, Minitab uses a procedure called the Hamiltonian Walk, which is a method for calculating all possible subsets of predictors, one subset per step. That is, Minitab calculates all 2**m - 1 subsets in 2**m - 1 steps, where m is the number of predictors in the model. Minitab evaluates a different subset regression at each step.
Each subset in the Hamiltonian Walk differs from the preceding subset by the addition or deletion of only one variable. The sweep operator "sweeps" a variable in or out of the regression on each step of the Hamiltonian Walk, and calculates the R2 for each subset.
Regression equation
For a model with multiple predictors, the equation is:
y = β0 + β1x1 + … + βkxk + ε
The fitted equation is:
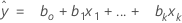
In simple linear regression, which includes only one predictor, the model is:
y=ß0+ ß1x1+ε
Using regression estimates b0 for ß0, and b1 for ß1, the fitted equation is:
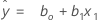
Notation
| Term | Description |
|---|---|
| y | response |
| xk | kth term. Each term can be a single predictor, a polynomial term, or an interaction term. |
| ßk | kth population regression coefficient |
| ε | error term that follows a normal distribution with a mean of 0 |
| bk | estimate of kth population regression coefficient |
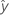 | fitted response |
R-sq
R2 is also known as the coefficient of determination.
Formula

Notation
| Term | Description |
|---|---|
| yi | i th observed response value |
 | mean response |
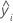 | i th fitted response |
R-sq (adj)

Notation
| Term | Description |
|---|---|
| MS | Mean Square |
| SS | Sum of Squares |
| DF | Degrees of Freedom |
PRESS
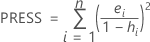
Notation
| Term | Description |
|---|---|
| n | number of observations |
| ei | ith residual |
| hi | ith diagonal element of X (X' X)-1X' |
R-sq (pred)
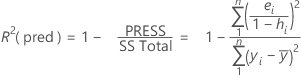
While the calculations for R2(pred) can produce negative values, Minitab displays zero for these cases.
Notation
| Term | Description |
|---|---|
| yi | i th observed response value |
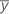 | mean response |
| n | number of observations |
| ei | i th residual |
| hi | i th diagonal element of X(X'X)–1X' |
| X | design matrix |
Mallows' Cp
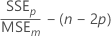
Notation
| Term | Description |
|---|---|
| SSEp | sum of squared errors for the model under consideration |
| MSEm | mean square error for the model with all candidate terms |
| n | number of observations |
| p | number of terms in the model, including the constant |
S

Notation
| Term | Description |
|---|---|
| MSE | mean square error |
Log-likelihood

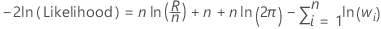
Observations with weights of 0 are not in the analysis.
Notation
| Term | Description |
|---|---|
| n | the number of observations |
| R | the sum of squares for error for the model |
| wi | the weight of the ith observation |
AICc (Akaike's Corrected Information Criterion)
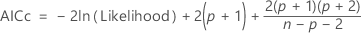
AICc is not calculated when  .
.
Notation
| Term | Description |
|---|---|
| n | the number of observations |
| p | the number of coefficients in the model, including the constant |
BIC (Bayesian Information Criterion)

Notation
| Term | Description |
|---|---|
| p | the number of coefficients in the model, including the constant |
| n | the number of observations |
Condition number

Notation
| Term | Description |
|---|---|
| C | the condition number |
| λmaximum | the maximum eigenvalue from the correlation matrix of the terms in the model, not including the intercept |
| λminimum | the minimum eigenvalue from the correlation matrix of the terms in the model, not including the intercept |
