Note
This command is available with the Predictive Analytics Module. Click here for more information about how to activate the module.
A Random Forests® model is an approach to solving classification and regression problems. The approach is both more accurate and more robust to changes in predictor variables than a single classification or regression tree. A broad, general description of the process is that Minitab Statistical Software builds a single tree from a bootstrap sample. Minitab randomly selects a smaller number of predictors out of the total number of predictors to evaluate the best splitter at each node. Minitab repeats this process to grow many trees. In the classification case, the classification from each tree is a vote for the predicted classification. For a given row of the data, the class with the most votes is the predicted class for that row in the data set.
To build a classification tree, the algorithm uses the Gini criterion to measure the impurity of nodes. For the desktop application, each tree grows until a node is impossible to split or a node reaches the minimum number of cases to split an internal node. The mimimum number of cases is an option for the analysis. For the web app, the analysis adds the constraint that each tree has a limit of 4,000 terminal nodes. For more details on the construction of a classification tree, go to Node splitting methods in CART® Classification. Details that are specific to Random Forests® follow.
Bootstrap samples
To build each tree, the algorithm selects a random sample with replacement (bootstrap sample) from the full data set. Usually, each bootstrap sample is different and can contain a different number of unique rows from the original data set. If you use only out-of-bag validation, then the default size of the bootstrap sample is the size of the original data set. If you divide the sample into a training set and a test set, then the default size of the bootstrap sample is the same as the size of the training set. In either case, you have the option to specify that the bootstrap sample is smaller than the default size. On average, a bootstrap sample contains about 2/3 of the rows of data. The unique rows of data that are not in the bootstrap sample are the out-of-bag data for validation.
Random selection of predictors
At each node in the tree, the algorithm randomly selects a subset of the
total number of predictors,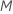 
,
to evaluate as splitters. By default, the algorithm chooses
predictors to evaluate at each node. You have the option to choose a different
number of predictors to evaluate, from 1 to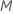 
.
If you choose 
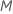predictors, then the algorithm evaluates every predictor at every node,
resulting in an analysis with the name "bootstrap forest."
In an analysis that uses a subset of predictors at each node, the evaluated predictors are usually different at each node. The evaluation of different predictors makes the trees in the forest less correlated with each other. The less-correlated trees create a slow learning effect so that the predictions improve as you build more trees.
Validation with out-of-bag data
The unique rows of data that are not part of the tree-building process for a given tree are the out-of-bag data. Calculations for measures of model performance, such as the average –log likelihood, make use of the out-of-bag data. For more details, go to Methods and formulas for the model summary in Random Forests® Classification.
For a given tree in the forest, a class vote for a row in the out-of-bag data is the predicted class for the row from the single tree. The predicted class for a row in out-of-bag data is the class with the highest vote across all trees in the forest.
The predicted class probability for a row in the out-of-bag data is the ratio of the number of votes for the class and the total votes for the row. Model validation uses the predicted classes, predicted class probabilities, and actual response values for all rows that appear at least once in the out-of-bag data.
Determination of the predicted class for a row in the training set
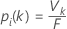
where Vk is the number of trees that vote that row i is in class k and F is the number of trees in the forest.
