Model summary table for MARS® Regression

Total predictors

The number of total predictors available for the model. This is the sum of the continuous predictors and the categorical predictors that you specify.

Important predictors

The number of important predictors in the model. Important predictors are the variables that have at least 1 basis function in the model.

Interpretation

You can use the Relative Variable Importance plot to display the order of relative variable importance. For instance, suppose 10 of 20 predictors have basis functions in the model, the Relative Variable Importance plot displays the variables in importance order.

Maximum number of basis functions

The number of basis functions that the algorithm builds to search for the optimal model.

Interpretation

By default, Minitab Statistical Software sets the maximum number of basis functions to 30. Consider a larger value when 30 basis functions seems too small for the data. For example, consider a larger value when you believe that more than 30 predictors are important.

Optimal number of basis functions

The number of basis functions in the optimal model.

Interpretation

After the analysis estimates the model with the maximum number of basis functions, the analysis uses a backwards elimination procedure to remove basis functions from the model. One-by-one, the analysis removes the basis function that contributes the least to the model fit. At each step, the analysis calculates the value of the optimality criterion for the analysis, either R-squared or mean absolute deviation. After the elimination procedure is complete, the optimal number of basis functions is the number from the elimination procedure that produces the optimal value of the criterion.

R-squared

R² is the percentage of variation in the response that the model explains. Outliers have a greater effect on R² than on MAD and MAPE.

When you use a validation method, the table includes an R² statistic for the training data set and an R² statistic for the test data set. When the validation method is k-fold cross-validation, the test data set is each fold when the model building excludes that fold. The test R² statistic is typically a better measure of how the model works for new data.

Interpretation

Use R² to determine how well the model fits your data. The higher the R² value, the better the model fits your data. R² is always between 0% and 100%.

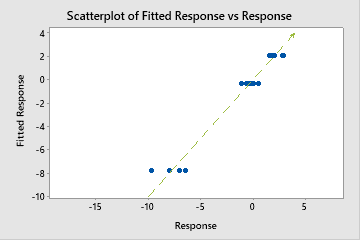
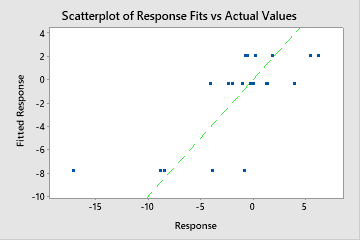
You can graphically illustrate the meaning of different R² values. The first plot illustrates a simple regression model that explains 85.5% of the variation in the response. The second plot illustrates a model that explains 22.6% of the variation in the response. The more variation that is explained by the model, the closer the data points fall to the fitted values. Theoretically, if a model can explain 100% of the variation, the fitted values would always equal the observed values and all of the data points would fall on the line y = x.

A test R² that is substantially less than the training R² indicates that the model might not predict the response values for new cases as well as the model fits the current data set.

Root mean square error (RMSE)

The root mean square error (RMSE) measures the accuracy of the model. Outliers have a greater effect on RMSE than on MAD and MAPE.

When you use a validation method, the table includes an RMSE statistic for the training data set and an RMSE statistic for the test data set. When the validation method is k-fold cross-validation, the test data set is each fold when the model building excludes that fold. The test RMSE statistic is typically a better measure of how the model works for new data.

Interpretation

Use to compare the fits of different models. Smaller values indicate a better fit. A test RMSE that is substantially less than the training RMSE indicates that the model might not predict the response values for new cases as well as the model fits the current data set.

Mean squared error (MSE)

The mean square error (MSE) measures the accuracy of the model. Outliers have a greater effect on MSE than on MAD and MAPE.

When you use a validation method, the table includes an MSE statistic for the training data set and an MSE statistic for the test data set. When the validation method is k-fold cross-validation, the test data set is each fold when the model building excludes that fold. The test MSE statistic is typically a better measure of how the model works for new data.

Interpretation

Use to compare the fits of different models. Smaller values indicate a better fit. A test MSE that is substantially less than the training MSE indicates that the model might not predict the response values for new cases as well as the model fits the current data set.

Mean absolute deviation (MAD)

The mean absolute deviation (MAD) expresses accuracy in the same units as the data, which helps conceptualize the amount of error. Outliers have less of an effect on MAD than on R², RMSE, and MSE.

When you use a validation method, the table includes an MAD statistic for the training data set and an MAD statistic for the test data set. When the validation method is k-fold cross-validation, the test data set is each fold when the model building excludes that fold. The test MAD statistic is typically a better measure of how the model works for new data.

Interpretation

Use to compare the fits of different models. Smaller values indicate a better fit. A test MAD that is substantially less than the training MAD indicates that the model might not predict the response values for new cases as well as the model fits the current data set.