Row and column contributions for Simple Correspondence Analysis

Column profiles lie in a d-dimensional space. The full set of d principal axes span this space. Suppose g_j1, g_j2, g_j3, ..., g_jd are the coordinates of column profile j in terms of the principal axes. These coordinates are called the column principal coordinates. The k^th principal coordinate for column profile j is g_jk.

The best k-dimensional subspace is spanned by the first k principal axes. If we project column profile j onto the best k-dimensional subspace, g_j1, ..., g_jk are the column principal coordinates of the profile in this subspace.

Each principal axis contributes to the inertia of each row. The correlation for row i and component k is the contribution of principal axis k to the row i inertia, expressed as a percent of the inertia for row i.

Correlation can also be viewed as the correlation between row profile i and principal component k. This correlation is calculated as follows:

Similarly, the correlation for column j and component k is the contribution of principal axis k to column j, expressed as a percent of the inertia for column j.

Correlation can also be viewed as the correlation between column profile j and principal component k. This correlation is calculated as follows:

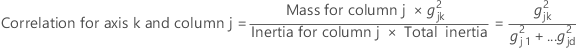
Minitab displays the relative inertia for a given row or column. The absolute inertia is the product of the relative inertia and the total inertia.

The sum of the correlations for row i (column j), over all principal components is 1. The sum over the first k principal coordinates is the quality associated with row profile i (column profile j) and the best k-dimensional subspace.

Notation

The inertia in a cell is calculated as follows:

The sum of all the cell inertias is the total inertia, sometimes simply called the inertia, for the table.

The relative inertia for a cell is calculated as follows:

Row profiles lie in a c-dimensional space. Lower dimensional subspaces are spanned by principal axes, also called principal components. The first principal axis is chosen as the vector in c-dimensional space that accounts for the maximum amount of the total inertia. Therefore, the first principal axis spans the best (that is, closest to the profiles using an appropriate metric) 1-dimensional subspace. The second principal axis is chosen as the vector in c-dimensional space that accounts for the maximum amount of the remaining inertia. Therefore, the first two principal axes span the best 2-dimensional subspace. The third principal axis is chosen as the vector in c-dimensional space that accounts for the maximum amount of the remaining inertia, after the inertia accounted for by the first two principal axes. Therefore, the first three principal axes span the best 3-dimensional subspace, and so on.

Let d = the smaller of (r − 1) and (c − 1). The row profiles (or equivalently the column profiles) actually lie in a d-dimensional subspace of the full c-dimensional space (or equivalently the full r-dimensional space). Thus, the number of principal axes is at most d.

The quality associated with row profile i and the best k-dimensional subspace is calculated as follows:

The quality associated with column profile j and the best k-dimensional subspace is calculated as follows:

Quality is always a number between 0 and 1, with larger numbers indicating a better approximation.

Notation

Each row contributes to the inertia of each axis. The contribution of row i to axis k, expressed as a percent of the inertia for axis k, is calculated as follows:

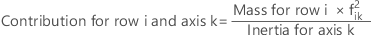
The sum of the contributions for principal axis k, over all rows i, is 1.

Similarly, each column contributes to the inertia of each axis. The contribution of column j to axis k, expressed as a percent of the inertia for axis k, is calculated as follows:

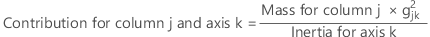
The sum of the contributions for principal axis k, over all columns j is 1.

Notation

The mass for row i is calculated as follows:

The mass for column j is calculated as follows:

The vector of r row masses is the same as the average row profile and the vector of c column masses is the same as the average column profile.