Average
In average linkage, the distance between two clusters is the average distance between a variable in one cluster and a variable in the other cluster. The average distance is calculated with the following distance matrix:

Notation
| Term | Description |
|---|---|
| dmj | distance between clusters m and j |
| m | merged cluster that consists of clusters k and l, with m = (k,i) |
| dkj | distance between clusters k and j |
| dlj | distance between clusters l and j |
| Nk | number of variables cluster k |
| Nl | number of variables in cluster l |
| Nm | number of variables in cluster m |
Centroid
In centroid linkage, the distance between two clusters is the distance between the cluster centroids or means. The distance is calculated with the following distance matrix:
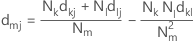
Notation
| Term | Description |
|---|---|
| dmj | distance between clusters m and j |
| m | merged cluster that consists of clusters k and l, with m = (k,i) |
| dkj | distance between clusters k and j |
| dlj | distance between clusters l and j |
| Nk | number of variables cluster k |
| Nl | number of variables in cluster l |
| Nm | number of variables in cluster m |
Complete
With the complete linkage method (also called furthest neighbor method), the distance between two clusters is the maximum distance between a variable in one cluster and a variable in the other cluster. The complete distance is calculated with the following distance matrix:
dmj = max (dkj, dlj)
Notation
| Term | Description |
|---|---|
| dmj | distance between clusters m and j |
| m | merged cluster that consists of clusters k and l, with m = (k,i) |
| dkj | distance between clusters k and j |
| dlj | distance between clusters l and j |
McQuitty
With McQuitty's linkage method, the distance is calculated with the following distance matrix:
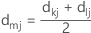
Notation
| Term | Description |
|---|---|
| dmj | distance between clusters m and j |
| m | merged cluster that consists of clusters k and l, with m = (k,i) |
| dkj | distance between clusters k and j |
| dlj | distance between clusters l and j |
Median
In median linkage, the distance between two clusters is the median distance between a variable in one cluster and a variable in the other cluster. The median distance is calculated with the following distance matrix:
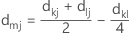
Notation
| Term | Description |
|---|---|
| dmj | distance between clusters m and j |
| m | merged cluster that consists of clusters k and l, with m = (k,i) |
| dkj | distance between clusters k and j |
| dlj | distance between clusters l and j |
| dkl | distance between clusters k and l |
Single
With the single linkage method (also called nearest neighbor method), the distance between two clusters is the minimum distance between a variable in one cluster and a variable in the other cluster.
The distance is calculated with the following distance matrix:
dmj = min (dkj, dlj)
Notation
| Term | Description |
|---|---|
| dmj | distance between clusters m and j |
| m | merged cluster that consists of clusters k and l, with m = (k,i) |
| dkj | distance between clusters k and j |
| dlj | distance between clusters l and j |
Ward
In Ward's linkage, the distance between two clusters is the sum of squared deviations from points to centroids. The objective of Ward's linkage is to minimize the within-cluster sum of squares. The distance is calculated with the following distance matrix:
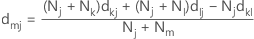
Note
In Ward's linkage, the distance between two clusters can be larger than d(max), the maximum value in the original distance matrix, D. If this happens, the similarity will be negative.
Notation
| Term | Description |
|---|---|
| dmj | distance between clusters m and j |
| m | merged cluster that consists of clusters k and l, with m = (k,i) |
| dkj | distance between clusters k and j |
| dlj | distance between clusters l and j |
| dkl | distance between clusters k and l |
| Nj | number of variables in cluster j |
| Nk | number of variables in cluster k |
| Nl | number of variables in cluster l |
| Nm | number of variables in cluster m |
