Definitive screening designs

Definitive screening designs are resolution IV designs. In a resolution IV design, terms for main effects are not aliased with 2-way interactions. In definitive screening designs, 2-way interactions are usually partly confounded with each other and square terms, but you can still estimate some 2-way interactions. Square terms are not aliased with terms for main effects, so you can estimate some square terms. In many cases, you can estimate all 2-way interactions and square terms that involve any 3 factors in the experiment. For more information on aliasing, go to What are confounding and alias structure?.

Definitive screening designs are a type of resolution IV design. In resolution IV designs, main effects are not aliased with any 2-way interactions. Because resolution III designs have relatively few runs when you compare them to more detailed designs, resolution III designs are common screening designs. However, in resolution III designs main effects are aliased with 2-way interactions.

Consider a definitive screening design when you want to use extra runs so that main effects are not aliased with any 2-way interactions. To create a definitive screening design, use Stat > DOE > Screening > Create Screening Design. Consider a resolution III design when you are willing to assume that 2-way interactions are negligible during screening. To create a resolution III design, use Stat > DOE > Factorial > Create Factorial Design and select either a Plackett-Burman design or a 2-level factorial design.

Definitive screening designs include runs that are not in 2-level designs so that you can use definitive screening designs to estimate square terms. Square terms account for curvature in the response. An example of a curved relationship is the amount of nitrogen in soil and the amount of fruit a plant produces. The addition of the right amount of nitrogen increases fruit production, but the addition of too much nitrogen decreases fruit production. In definitive screening designs, no square terms are aliased with terms for main effects.

Besides definitive screening designs, 2 common types of screening designs are Plackett-Burman designs and resolution III fractional factorial designs. Both Plackett-Burman designs and resolution III fractional factorial designs are 2-level designs. From a 2-level design, you cannot estimate any square terms.

Plackett-Burman designs and fractional factorial designs can include center points. However, the addition of center points to these designs aliases all of the quadratic effects together. From a design with center points, you can assess whether the effect of at least 1 factor has a curved relationship with the response. However, you cannot distinguish any of the square terms from each other.

Consider a definitive screening design when you want to use extra runs to include square terms in the screening. To create a definitive screening design, use Stat > DOE > Screening > Create Screening Design. Consider a 2-level design to assess whether any square terms are important before you use runs to estimate the square terms. To create a 2-level design, use Stat > DOE > Factorial > Create Factorial Design.

Engineers are developing a new ultrasonic cleaner. The engineers use a screening design to determine which potential factors affect the output power for the cleaner.

The engineers consider a resolution III fractional factorial and a definitive screening design because they expect that an adequate model could have a square term for 1 or more factors. The resolution III fractional factorial design has only 11 runs in a single replicate with 3 center points. However, if the engineers need to add axial runs to estimate square terms, the resolution III fractional factorial design grows to 25 runs. The engineers decide to use a definitive screening design that can estimate the square terms with 17 runs.

After the experiment, one of the engineers analyzes the definitive screening design to determine the most important effects. The engineer looks at a Pareto chart of standardized effects from a model with the main effects. The chart also includes effects that are not in the model. In the pareto chart, A and D are the most important factors. None of the other factors have large main effects.

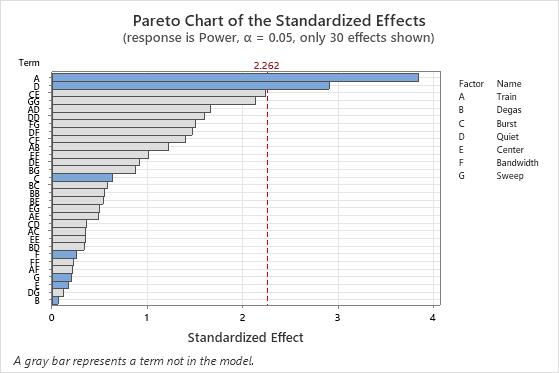
Because B was the smallest term in the model on the Pareto chart, the engineer excludes B from the model. The engineer looks at the Pareto chart without B in the model. In the second pareto chart, the engineer notices that the effects for a 2-way interaction (CE) and a square term (GG) cross the reference line, although the terms are not in the model.

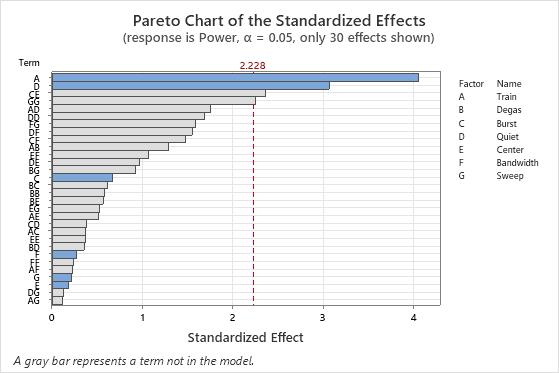
The engineer refines the model further and finds that the CE interaction and the GG square term remain statistically significant when the model includes those terms. The engineer decides that factors B and F do not have large main effects and are not likely to be in any large 2-way interactions. The engineer decides that the result of the screening experiment is that the engineer can exclude factors B and F in further experiments to understand the process better.