Which standard designs can Minitab create?

Minitab offers many different designed experiments to meet your needs.

In This Topic

Screening designs
Factorial designs
Response surface designs
Mixture designs
Taguchi designs

Screening designs

A type of designed experiment that is frequently used to determine the most important factors in a process. With a screening design, you use a relatively small number of runs with many potential factors to determine a smaller number of most important factors that affect process quality. After screening experiments, you can do optimization experiments if you need more detail. For example, say you are examining the various factors that affect ice cream texture: fat content, pasteurization temperature, homogenization process, mixing speed, draw temperature, emulsifier, stabilizer, and cooling speed. You can use a screening design to identify the most important factors that affect ice cream texture. If necessary, you can use a larger factorial design or a response surface design to optimize your process.

Minitab provides two types of designs that are usually used for screening. In some cases, you can also consider a fractional factorial design. For more information on screening designs, go to Screening designs.

Definitive screening designs: Definitive screening designs are screening designs that contain 3 levels per continuous factor so that they can estimate square terms as well as linear terms. Because linear terms are not aliased with any 2-factor interactions, a definitive screening design allows you to find evidence of potentially important interactions as well. For example, with 8 factors, the definitive screening design can fit all linear, square, and 2-way interactions efficiently for 3 or fewer important factors.
Plackett-Burman designs: Plackett-Burman designs are usually resolution III, 2-level designs. In a resolution III design, main effects are aliased with 2-way interactions. Therefore, you should only use these designs when you are willing to assume that 2-way interactions are negligible. Because of this assumption, Plackett-Burman designs can have fewer runs than definitive screening designs. If you suspect an interaction after you complete a Plackett-Burman design, you can fold the design, which doubles the number of runs. After you fold a Plackett-Burman design, main effects are not aliased with 2-way interactions. For more information, go to What is folding?.

Factorial designs

Factorial designs have many different uses, including the estimation of complex interactions and screening. With a factorial design, you can estimate the significance of main effects and interaction effects. You can also check for the presence of square terms. To estimate square terms, you usually add axial points to create a response surface design. For more information on factorial designs, go to Factorial and fractional factorial designs.

2-level factorial design (default generators)

Choose this option to create a full factorial design or to create a fractional factorial design. The default generators create the design with the highest resolution for the number of factors and the number of runs.

2-level factorial design (specify generators)

You can use your own generators to specify which subset of runs to include in a fractional factorial design. You can also specify generators to add factors and define blocks by specifying the generators for the terms.

2-level split-plot design (hard-to-change factors)

A designed experiment that includes at least one hard-to-change factor that is difficult to completely randomize due to time or cost constraints.

Plackett-Burman design

Plackett-Burman designs are usually resolution III, 2-level designs. In a resolution III design, main effects are aliased with 2-way interactions. Therefore, you should only use these designs when you are willing to assume that 2-way interactions are negligible.

Use Plackett-Burman designs to identify the most important factors in the early phases of experimentation. For example, say you are examining the various factors that affect ice cream texture: fat content, pasteurization temperature, homogenization process, mixing speed, draw temperature, emulsifier, stabilizer, and cooling speed. You can use a Plackett-Burman experiment to identify the most important main effects, use fractional or full factorial designs to study them more, then use response surface designs to optimize your process.

General full factorial design

A designed experiment in which the factors can have any number of levels. The factors are all categorical.

Response surface designs

A set of advanced design of experiments techniques that help you better understand your response. You often use response surface designs in sequential experimentation. First, you use a factorial design with center points to determine important factors and check for curvature. Then, if the results of the factorial design suggest curvature, you add axial points to the factorial design to create a type of response surface design called a central composite design.

Central composite: An experimental design that models curvature by adding center and axial points to a 2-level factorial design.
Box-Behnken: Box-Behnken designs usually have fewer design points than central composite designs, thus, they are less expensive to run with the same number of factors. They can efficiently estimate the first- and second-order coefficients; however, they can't include runs from a factorial experiment. Box-Behnken designs always have 3 levels per factor, unlike central composite designs which can have up to 5. Also unlike central composite designs, Box-Behnken designs never include runs where all factors are at their extreme setting, such as all of the low settings.

Mixture designs

Mixture experiments are a special class of response surface experiments in which the product under investigation is made up of several components or ingredients. Designs for these experiments are useful because many product design and development activities in industrial situations involve formulations or mixtures. In these situations, the response is a function of the proportions of the different ingredients in the mixture. For example, you might be developing a pancake mixture that is made of flour, baking powder, milk, eggs, and oil. Or, you might be developing an insecticide that blends four chemical ingredients. For more information on mixture designs, go to What is a mixture design?

In the simplest mixture experiment, the response (the quality or performance of the product based on some criterion) depends on the relative proportions of the components (ingredients). The amount of components, measured in weights, volumes, or some other units, add up to a common total. In contrast, in a factorial design, the response varies depending on the amount of each factor.

	Unaugmented	Augmented
Simplex Centroid	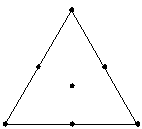You can fit up to a special cubic model.	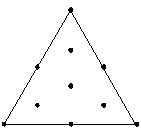You can partially fit up to a full cubic model.
Simplex Lattice Degree 1	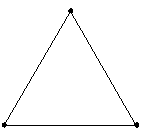You can fit a linear model.	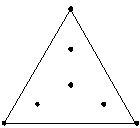You can partially fit up to a quadratic model.
Simplex Lattice Degree 2	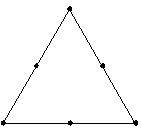You can fit up to a quadratic model.	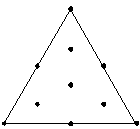You can partially fit up to a special cubic model.
Simplex Lattice Degree 3	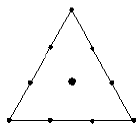You can fit up to a full cubic model.	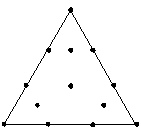You can fit up to a full cubic model.

Simplex centroid

Mixture designs in which the design points are arranged in a uniform manner (or lattice) over an L-simplex. With a simplex centroid design, you can estimate terms up to the same order as the number of components. For a smaller design, you can use a simplex lattice that limits the terms you estimate to a lower order.

Simplex lattice

Mixture designs in which the design points are arranged in a uniform manner (or lattice) over an L-simplex. The degree of the lattice determines the order of the terms that you can fit.

The 1 degree lattice has fewer runs than the simplex centroid design, but you can estimate only a simple model.

The 1 degree lattice has more runs than the simplex centroid design, so you can estimate a more complicated model.

Extreme vertices

Mixture designs that cover only a subportion or smaller space within the simplex.

The goal of an extreme vertices design is to choose design points that adequately cover the design space. The following figure shows the extreme vertices for two three-component designs with both upper and lower constraints:

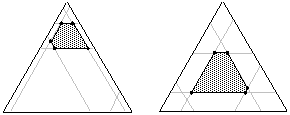
The light gray lines represent the lower and upper bound constraints on the components. The dark gray area represents the design space. The points are put at the extreme vertices of design space.

Taguchi designs

A Taguchi design is a designed experiment that lets you choose a product or process that functions more consistently in the operating environment. Taguchi designs recognize that not all factors that cause variability can be controlled. These uncontrollable factors are called noise factors. Taguchi designs try to identify controllable factors (control factors) that minimize the effect of the noise factors. During experimentation, you manipulate noise factors to force variability to occur and then determine optimal control factor settings that make the process or product robust, or resistant to variation from the noise factors. A process designed with this goal will produce more consistent output. A product designed with this goal will deliver more consistent performance regardless of the environment in which it is used.

A well-known example of Taguchi designs is from the Ina Tile Company of Japan in the 1950s. The company was manufacturing too many tiles outside specified dimensions. A quality team discovered that the temperature in the kiln used to bake the tiles varied, causing nonuniform tile dimension. They could not eliminate the temperature variation because building a new kiln was too costly. Thus, temperature was a noise factor. Using Taguchi designed experiments, the team found that by increasing the clay's lime content, a control factor, the tiles became more resistant, or robust, to the temperature variation in the kiln, letting them manufacture more uniform tiles.

2-level design: A designed experiment where each control factor has only 2 levels.
3-level design: A designed experiment where each control factor has exactly 3 levels.
4-level design: A designed experiment where each control factor has exactly four levels.
5-level design: A designed experiment where each control factor has exactly 5 levels.
Mixed level design: A designed experiment where the control factors have different numbers of levels.