In general, coefficients can be calculated from this formula:
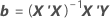
| Term | Description |
|---|---|
| X | the design matrix |
| Y | the response vector |
For a balanced, orthogonal design with no covariates, coefficients for main effects have a simple relationship to factor means. The following table of data means lets you calculate the coefficients for this simple case:
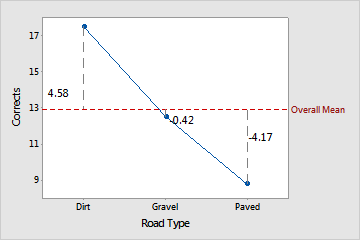
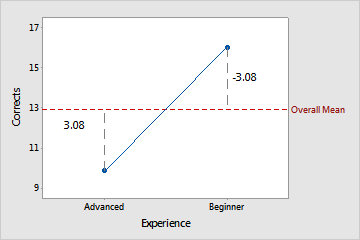
There is one main effect coefficient for each level of each factor. In the case that the factor coding in the design matrix is (-1, 0, 1), the coefficient is the mean for that level minus the overall mean. For example, the mean of the observations for RoadType: Dirt is 4.58 from the overall mean, while the mean of the observations for RoadType: Gravel is - 0.42 from the overall mean. The vertical lines in the plots show the coefficients for the driving data.
| Factor/Level | Mean | Effect |
|---|---|---|
| Experience: Advanced | 16 | 16 – 12.92 = 3.08 |
| Experience: Beginner | 9.83 | 9.83 – 12.92 = -3.08 |
| RoadType: Dirt | 17.5 | 17.5 - 12.92 = 4.58 |
| RoadType: Gravel | 12.5 | 12.5 - 12.92 = -0.42 |
| RoadType: Paved | 8.75 | 8.75 - 12.92 = -4.17 |
Notice that the effects for each factor add up to 0, except for rounding error.
