Methods and formulas for the diagnostic measures in Analyze Binary Response for Definitive Screening Design

In This Topic

Pearson residuals
Standardized and deleted Pearson residuals
Deviance residuals
Standardized deviance residual
Deleted deviance residual
Delta chi-square
Delta deviance
Delta beta (standardized)
Delta beta
Leverages
Cook's distance
DFITS
Variance inflation factor (VIF)

Pearson residuals

Elements of the Pearson chi-square that can be used to detect ill-fitted factor/covariate patterns. Minitab stores the Pearson residual for the i^th factor/covariate pattern. The formula is:

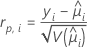
Notation

Term	Description
y_i	the response value for the i^th factor/covariate pattern
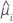	the fitted value for the i^th factor/covariate pattern
V	the variance function for the model at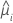

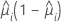
The following equation gives the variance function for a binomial model:

Standardized and deleted Pearson residuals

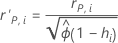
Used to detect ill-fitted factor/covariate patterns. Minitab stores the standardized Pearson residual for the i^th factor/covariate pattern. Deleted Pearson residuals are also called likelihood ratio Pearson residuals. For the deleted Pearson residual, Minitab calculates the one-step approximation described in Pregibon.¹ This approximation is equal to the standardized Pearson residual. The formula is:

Notation

Term	Description
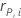	the Pearson residual for the i^th factor/covariate pattern
	1, for binomial models
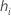	the leverage for the i^th factor/covariate pattern

Deviance residuals

Deviance residuals are based on the model deviance and are useful in identifying ill-fitted factor/covariate patterns. The model deviance is a goodness-of-fit statistic based on the log-likelihood function. The deviance residual defined for the i^th factor/covariate pattern is:

Notation

Term	Description
y_i	the response value for the i^th factor/covariate pattern
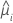	the fitted value for the i^th factor/covariate pattern
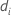	the deviance for the i^th factor/covariate pattern

Standardized deviance residual

The standardized deviance residual is helpful in the identification of outliers. The formula is:

Notation

Term	Description
r_D,i	The deviance residual for the i^th factor/covariate pattern
h_i	The leverage for the i^th factor/covariate pattern

Deleted deviance residual

The deleted deviance residual measures the change in the deviance due to the omission of the i^th case from the data. Deleted deviance residuals are also called likelihood ratio deviance residuals. For the deleted deviance residual, Minitab calculates a one-step approximation based on the Pregibon one-step approximation method¹. The formula is as follows:

Notation

Term	Description
y_i	the response value at the i^th factor/covariate pattern
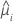	the fitted value for the i^th factor covariate pattern
h_i	the leverage for the i^th factor/covariate pattern
r'_D,i	the standardized deviance residual for the i^th factor/covariate pattern
r'_P,i	the standardized Pearson residual for the i^th factor/covariate pattern

1. Pregibon, D. (1981). "Logistic Regression Diagnostics." The Annals of Statistics, Vol. 9, No. 4 pp. 705–724.

Delta chi-square

Minitab calculates the change in the Pearson chi-square due to deleting all the observations with the j^th factor/covariate pattern. Minitab stores one delta chi-square value for each distinct factor/covariate pattern in the data. You can use delta chi-square to detect ill-fitted factor/covariate patterns. The formula for the delta chi-square is:

Formula

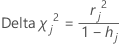
Notation

Term	Description
h_j	leverage
r_j	Pearson residuals

Delta deviance

Minitab calculates the change in the deviance statistic by deleting all the observations with the j^th factor/covariate pattern. Minitab stores one value for each distinct factor/covariate pattern in the data. You can use delta deviance to detect ill-fitted factor/covariate patterns. The change in the deviance statistic is:

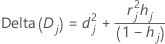
Notation

Term	Description
h_j	leverage
r_j	Pearson residuals
d_j	deviance residuals

Delta beta (standardized)

Minitab calculates the change by deleting all observations with the j^th factor/covariate pattern. One value is stored for each distinct factor/covariate pattern in the data. You can use standardized delta β to detect factor/covariate patterns that have a strong influence on the estimates of the coefficients. This value is based on the standardized Pearson residual.

Formula

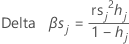
Notation

Term	Description
h_j	leverage
rs _j	standardized Pearson residuals

Delta beta

Minitab calculates the change by deleting all observations with the j^th factor/covariate pattern. One value is stored for each distinct factor/covariate pattern in the data. You can use delta β to detect factor/covariate patterns that have a strong influence on the estimates of the coefficients. This value is based on the Pearson residual.

Formula

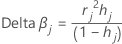
Notation

Term	Description
h_j	leverage
r_j	Pearson residuals

Leverages

The leverages are the diagonal elements of the generalized hat matrix. The leverages are useful in detecting factor/covariate patterns that may have a significant influence on the results.

Formula

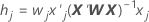
Notation

Term	Description
w_j	the j^th diagonal element of the weight matrix from fitting the coefficients
x_j	the j^th row of the design matrix
X	the design matrix
X'	the transpose of X
W	the weight matrix from the estimation of the coefficients

Cook's distance

Minitab calculates an approximate Cook's distance.

Formula

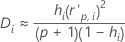
Notation

Term	Description
h_i	the leverage for the i^th factor/covariate pattern
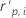	the standardized Pearson residual for the i^th factor/covariate pattern
p	the regression degrees of freedom

DFITS

A measure of the influence of a single deletion on the fitted values. Observations with large DFITS values may be outliers. Minitab calculates an approximate value for DFITS.

Formula

Notation

Term	Description
h_i	The leverage for the data point
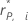	The deleted Pearson residual for the data point

Variance inflation factor (VIF)

To calculate a VIF, perform a weighted regression on the predictor with the remaining predictors. The weight matrix is that given in McCullagh and Nelder¹ for the estimation of the coefficients. In this case, the VIF formula is equivalent to the formula for a linear regression. For example, for predictor x_j the formula for the VIF is:

Notation

Term	Description
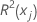	coefficient of determination with x_j as the response variable and the other terms in the model as the predictors

1. P. McCullagh and J. A. Nelder (1989). Generalized Linear Models, 2^nd Edition, Chapman & Hall/CRC, London.