In This Topic
What is alias structure?
The alias structure describes the confounding pattern that occurs in a design. Terms that are confounded are also said to be aliased.
Aliasing, also known as confounding, occurs in fractional factorial designs because the design does not include all of the combinations of factor levels. For example, if factor A is confounded with the 3-way interaction BCD, then the estimated effect for A is the sum of the effect of A and the effect of BCD. You cannot determine whether a significant effect is because of A, because of BCD, or because of a combination of both. When you analyze the design in Minitab, you can include confounded terms in the model. Minitab removes the terms that are listed later in the terms list. However, certain terms are always fit first. For example, if you include blocks in the model, Minitab retains the block terms and removes any terms that are aliased with blocks.
- If the design has 7 or fewer factors, then the alias structure shows all the terms that are aliased.
- If the design has 8–10 factors, then the alias structure shows the aliasing of terms up to and including 3-factor interactions.
- If the design has 11–15 factors, then the alias structure shows the aliasing of terms up to and including 2-factor interactions.
Alias structure for a fractional design
In a fractional factorial design, some terms for factors cannot be estimated separately from each other. Use the alias structure to examine the aliased terms.
Interpretation
- Surgeon: Whether the surgeon attends the patient throughout the hospitalization.
- VAS: Whether hospital staff use a visual analog scale to assess a patient's pain level.
- Ibuprofen: Whether ibuprofen is used to treat pain.
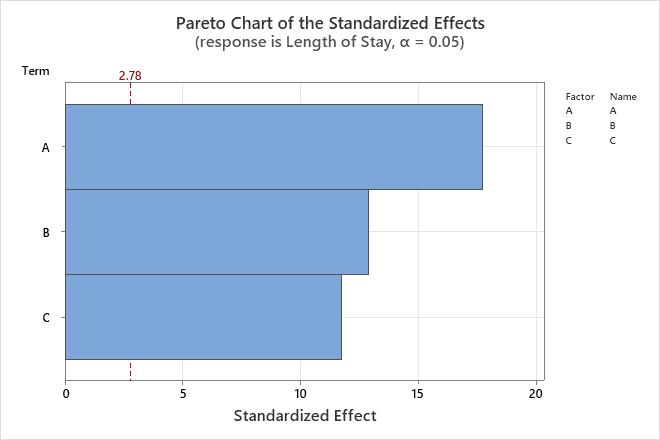
The Pareto chart of the effects indicates that all of the factors are statistically significant at the 0.05 level, but the alias structure shows that main effects are aliased with 2-factor interactions.
Alias Structure
| Factor | Name |
|---|---|
| A | Surgeon |
| B | VAS |
| C | Ibuprofen |
| Aliases |
|---|
| I + ABC |
| A + BC |
| B + AC |
| C + AB |
In these data, the effect labeled A on the Pareto chart could refer to either the Surgeon main effect, the Ibuprofen*VAS interaction effect, or some combination of both. Because of the aliasing, Minitab will not include both Factor A and the interaction between B and C in the same model. To distinguish these effects, the researchers can add more runs to the experiment by folding the design. For more information on folding, go to What is folding?.
Alias structure for a blocked design
When a design has more blocks than replicates, some terms are aliased with terms for blocks.
Interpretation
- Surgeon: Whether the surgeon attends the patient throughout the hospitalization.
- VAS: Whether hospital staff use a visual analog scale to assess a patient's pain level.
- Ibuprofen: Whether ibuprofen is used to treat pain.
Because the researchers cannot collect all of the data in a short amount of time, the researchers use blocks to account for differences that might occur between runs performed under different conditions, such as variation in the batch of cement for different patients. The alias structure shows that the terms for blocks are aliased with the term for the 3-factor interaction. When you analyze the design in Minitab, terms for blocks enter the model before interactions. Thus, if the terms for blocks are in the model, Minitab will not include the ABC interaction in the model.
Alias Structure
| Factor | Name |
|---|---|
| A | Surgeon |
| B | VAS |
| C | Ibuprofen |
| Aliases |
|---|
| I |
| Block 1 - ABC |
| Block 2 + ABC |
| Block 3 - ABC |
| A |
| B |
| C |
Alias structure for a design with partial aliasing
Aliasing occurs when the design does not include all of the combinations of factor levels. In the alias structure, fully-aliased terms have coefficients equal to 1. For example, if factor A is confounded with the 3-way interaction BCD, then the estimated effect for A is the sum of the effect of A and the effect of BCD. You cannot determine whether a significant effect is because of A, because of BCD, or because of a combination of both. If you try to include fully-aliased terms in the same model, Minitab removes the fully-aliased terms that are later in the terms list.
Partial aliasing occurs in factorial designs with covariates, factorial designs with binary responses, and Plackett-Burman designs. With partial aliasing, the terms in the alias structure have coefficients other than 1. Be cautious when you interpret terms with partial aliasing. The coefficient in the alias table shows how much that term biases the estimate of the term that is in the model.
Interpretation
- Surgeon: Whether the surgeon attends the patient throughout the hospitalization.
- VAS: Whether hospital staff use a visual analog scale to assess a patient's pain level.
- Ibuprofen: Whether ibuprofen is used to treat pain.
The covariate is the age of the patient. The age of a patient is an important variable in a patient's length of stay, but the researchers cannot control the patient's age for each experimental run. The alias structure shows that several interactions are partially aliased with other terms. For example, the second row shows that the main effect for A is partially aliased with the interactions AB, AC, BC, and ABC. The final row shows that the main effect for C is completely confounded with the AB interaction.
Alias Structure
| Factor | Name |
|---|---|
| A | Surgeon |
| B | VAS |
| C | Ibuprofen |
| Aliases |
|---|
| I + 0.91 AB - 0.23 AC - 1.37 BC + 0.27 ABC |
| A + 0.61 AB - 0.15 AC - 0.41 BC - 0.15 ABC |
| B + 0.04 AB + 0.49 AC - 0.07 BC - 0.01 ABC |
| C + AB |
