Analysis of variance table for Analyze Binary Response for Factorial Design

Find definitions and interpretation guidance for every statistic in the Analysis of variance table.

In This Topic

DF
Seq Dev
Contribution
Adj Dev
Adj Mean

Chi-Square
P-value – Model
P-Value – Term
P-value – Curvature

DF

The total degrees of freedom (DF) are the amount of information in your data. The analysis uses that information to estimate the values of the coefficients. The total DF is 1 less than the number of rows in the data. The DF for a term shows how many coefficients that term uses. Increasing the number of terms in your model adds more coefficients to the model, which decreases the DF for error. The DF for error are the remaining degrees of freedom that are not used in the model.

Note

For a 2-level factorial design or a Plackett-Burman design, if a design has center points, then one DF is for the test for curvature. If the term for center points is in the model, the row for curvature is part of the model. If the term for center points is not in the model, the row for curvature is part of the error that is used to test terms that are in the model. In response surface and definitive screening designs, you can estimate square terms, so the test for curvature is unnecessary.

Seq Dev

Sequential deviance measures the deviance for different components of the model. Unlike adjusted deviance, the sequential deviance depends on the order that the terms enter the model. In the Deviance table, Minitab separates the sequential deviance into different components that describe the deviance explained by different sources.

Model: The sequential deviance for the regression model quantifies how much of the total deviance is explained by the model.

Term: The sequential deviance for a term quantifies the difference between a model up to and including a particular term, with the term and without the term.
Error: The sequential deviance for error quantifies the deviance that the model does not explain.
Total: The total sequential deviance is the sum of the sequential deviance for the model and the sequential deviance for error. The total sequential deviance quantifies the total deviance in the data.

Interpretation

When you specify use of the sequential deviance for tests, Minitab uses the sequential deviance to calculate the p-values for the regression model and the individual terms. Usually, you interpret the p-values instead of the sequential deviance.

Contribution

Contribution displays the percentage that each source in the ANOVA table contributes to the total sequential deviance.

Interpretation

Higher percentages indicate that the source accounts for more of the deviance in the response variable. The percent contribution for the regression model is the same as the deviance R².

Adj Dev

Adjusted deviances are measures of variation for different components of the model. The order of the predictors in the model does not affect the calculation of the adjusted deviances. In the Deviance table, Minitab separates the deviance into different components that describe the deviance explained by different sources.

Model: The adjusted deviance for the regression model quantifies the difference between the current model and the constant model.
Term: The adjusted deviance for a term quantifies the difference between a model with the term and without the term.
Error: The adjusted deviance for error quantifies the deviance that the model does not explain.
Total: The total adjusted deviance is the sum of the adjusted deviance for the model and the adjusted deviance for error. The total adjusted deviance quantifies the total deviance in the data.

Interpretation

Minitab uses the adjusted deviances to calculate the p-value for a term. Minitab also uses the adjusted deviances to calculate the deviance R² statistic. Usually, you interpret the p-values and the R² statistic instead of the deviances.

Adj Mean

Adjusted mean deviance measures how much deviance a term or a model explains for each degree of freedom. The calculation of the adjusted mean deviance for each term assumes that all other terms are in the model.

Interpretation

Minitab uses the chi-square value to calculate the p-value for a term. Usually, you interpret the p-values instead of the adjusted mean squares.

Chi-Square

Each term in the ANOVA table has a chi-square value. The chi-square value is the test statistic that determines whether a term or model has an association with the response.

Interpretation

Minitab uses the chi-square statistic to calculate the p-value, which you use to make a decision about the statistical significance of the terms and the model. The p-value is a probability that measures the evidence against the null hypothesis. Lower probabilities provide stronger evidence against the null hypothesis. A sufficiently large chi-square statistic results in a small p-value, which indicates that the term or model is statistically significant.

P-value – Model

The p-value is a probability that measures the evidence against the null hypothesis. Lower probabilities provide stronger evidence against the null hypothesis.

Interpretation

To determine whether the data provide evidence that at least one coefficient in the regression model is different from 0, compare the p-value for regression to your significance level to assess the null hypothesis. The null hypothesis for the p-value for model is that all of the coefficients for terms in the regression model are 0. Usually, a significance level (denoted as α or alpha) of 0.05 works well. A significance level of 0.05 indicates a 5% risk of concluding that at least one coefficient is different from 0 when all of the coefficients are 0.

P-value ≤ α: At least one coefficient is different from 0: If the p-value is less than or equal to the significance level, you conclude that at least one coefficient is different from 0.
P-value > α: Not enough evidence exists to conclude that at least one coefficient is different from 0: If the p-value is greater than the significance level, you cannot conclude that at least one coefficient is different from 0. You may want to fit a new model.

The tests in the Deviance table are likelihood ratio tests. The test in the expanded display of the Coefficients table are Wald approximation tests. The likelihood ratio tests are more accurate for small samples than the Wald approximation tests.

P-Value – Term

The p-value is a probability that measures the evidence against the null hypothesis. Lower probabilities provide stronger evidence against the null hypothesis.

Interpretation

To determine whether the association between the response and each term in the model is statistically significant, compare the p-value for the term to your significance level to assess the null hypothesis. The null hypothesis is that there is no association between the term and the response. Usually, a significance level (denoted as α or alpha) of 0.05 works well. A significance level of 0.05 indicates a 5% risk of concluding that an association exists when there is no actual association.

P-value ≤ α: The association is statistically significant: If the p-value is less than or equal to the significance level, you can conclude that there is a statistically significant association between the response variable and the term.
P-value > α: The association is not statistically significant: If the p-value is greater than the significance level, you cannot conclude that there is a statistically significant association between the response variable and the term. You may want to refit the model without the term.; If there are multiple predictors without a statistically significant association with the response, you can reduce the model by removing terms one at a time. For more information on removing terms from the model, go to Model reduction.

If a model term is statistically significant, the interpretation depends on the type of term. The interpretations are as follows:

If a continuous factor is significant, you can conclude that the coefficient for the factor is different from zero.
If a categorical factor is significant, you can conclude that the probability of the event is not the same for all levels of the factor.
If an interaction term is significant, you can conclude that the relationship between a factor and the probability of the event depends on the other factors in the term.
If a quadratic term is significant, you can conclude that the response surface features curvature.

The tests in the Analysis of variance table are likelihood ratio tests. The test in the expanded display of the Coefficients table are Wald approximation tests. The likelihood ratio tests are more accurate for small samples than the Wald approximation tests.

P-value – Curvature

The p-value is a probability that measures the evidence against the null hypothesis. Lower probabilities provide stronger evidence against the null hypothesis.

Minitab tests for curvature when the design has center points. The test looks at the fitted mean of the response at the center points relative to the expected mean if the relationships between the model terms and the response are linear. To visualize the curvature, use factorial plots.

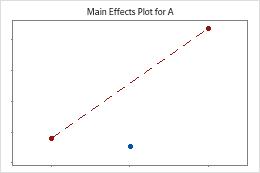
The center points are far away from the line that joins the means of the corner points, which suggests a curved relationship. Use the p-value to verify that the curvature is statistically significant.

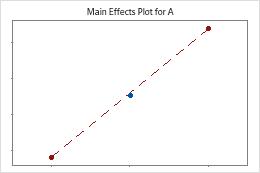
The center points are near the line that joins the means of the corner points. The curvature is probably not statistically significant.

Interpretation

To determine whether at least one of the factors have a curved relationship with the response, compare the p-value for curvature to your significance level to assess the null hypothesis. The null hypothesis is that all the relationships between the factors and the response are linear.

Usually, a significance level (denoted as α or alpha) of 0.05 works well. A significance level of 0.05 indicates a 5% risk of concluding that different conditions between runs change the response when the conditions do not.

P-value ≤ α: At least one factor has a curved relationship with the response: If the p-value is less than or equal to the significance level, you conclude that at least one of the factors has a curved relationship with the response. You may want to add axial points to the design so that you can model the curvature.
P-value > α: There is not enough evidence to conclude that any factors have a curved relationship with the response: If the p-value is greater than the significance level, you cannot conclude that any of the factors have a curved relationship with the response. If the curvature is part of the model, you may want to refit the model without a term for center points so that the curvature is part of the error.

Note

Usually, if the curvature is not statistically significant, you remove the center point term. If you leave the center points in the model, Minitab assumes that the model contains curvature that the factorial design cannot fit. Due to the inadequate fit, Contour Plot, Surface Plot, and Overlaid Contour Plot are not available. Also, Minitab does not interpolate between the factor levels in the design with Response Optimizer. For more information on ways to use the model, go to Stored model overview.