It is important to consider the family error rate when making multiple comparisons because your chances of making a type I error for a series of comparisons is greater than the error rate for any one comparison alone. To counter this higher error rate, Tukey's method adjusts the confidence level for each individual interval so that the resulting simultaneous confidence level is equal to the value you specify.
Example of Tukey confidence intervals
You are measuring the response times for memory chips. You sampled 25 chips from five different manufacturers.
You decide to examine all 10 comparisons between the five plants to determine specifically which means are different. Using Tukey's method, you specify that the entire set of comparisons should have a family error rate of 0.05 (equivalent to a 95% simultaneous confidence level). Minitab calculates that the 10 individual confidence levels need to be 99.35% in order to obtain the 95% joint confidence level. These wider Tukey confidence intervals provide less precise estimates of the population parameter but limit the probability that one or more of the confidence intervals does not contain the true difference to a maximum of 5%. Understanding this context, you can then examine the confidence intervals to determine whether any do not include zero, indicating a significant difference.
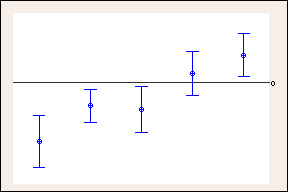
Confidence intervals with 95% individual confidence levels
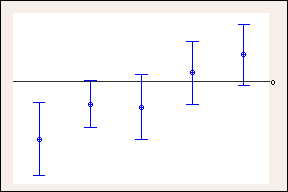
Confidence intervals with 99.35% individual confidence levels to obtain a 95% joint confidence level using Tukey's
Comparison of 95% confidence intervals to the wider 99.35% confidence intervals used by Tukey's in the previous example. The reference line at 0 shows how the wider Tukey confidence intervals can change your conclusions. Confidence intervals that contain zero indicate no difference. (Only 5 of the 10 comparisons are shown due to space considerations.)
