In This Topic
Variance components
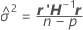
where 

For details on the estimation of θi, see [1].
For further details on the notation, go to the Methods section.
References
- Hemmerle, W. and Hartley, H. (1973). Computing Maximum Likelihood Estimates for the Mixed A.O.V. Model using the W transformation. Technometrics, 15(4):819–831.
Standard errors of variance components
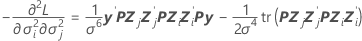
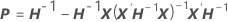
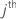 column, j = 1, …, c:
column, j = 1, …, c:
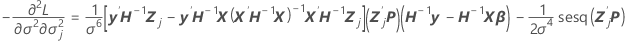

This component is also the value of the last column and the 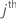 row by the symmetry property of the variance-covariance matrix.
row by the symmetry property of the variance-covariance matrix.

The asymptotic variance-covariance matrix for the variance components estimates is twice the inverse of the observed Fisher information matrix. The estimates of the standard errors are the square roots of the diagonal elements of the variance-covariance matrix. The first c diagonal elements are for the variance components of the random effect terms. The last diagonal element is for the error variance component.
Notation
| Term | Description |
|---|---|
 | the trace of matrix  |
 | the sum of squares of all the elements in the matrix M |
For further details on the notation, go to the Methods section.
Confidence intervals for variance components
Minitab uses the delta method to construct Wald-type confidence limits for the natural log of the variance components, then exponentiates the confidence intervals to get the confidence intervals for the variance components. The formulas for the variance component for error have the same form.
Two-sided interval
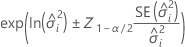
Lower bound
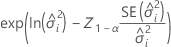
Upper bound
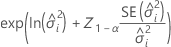
Notation
| Term | Description |
|---|---|
 | the 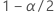 quantile from the standard normal distribution quantile from the standard normal distribution |
 | 1 − confidence level |
 | the standard error of the 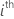 variance component variance component |
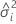 | the variance component for the 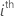 random effect term random effect term |
Z-value and p-value
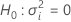
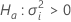


Notation
| Term | Description |
|---|---|
| Z | the value of the inverse cumulative distribution function for the standard normal distribution |
Variance-covariance matrix
 component of the observed Fisher information matrix:
component of the observed Fisher information matrix:
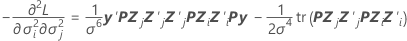

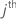 column, j = 1, …, c:
column, j = 1, …, c:
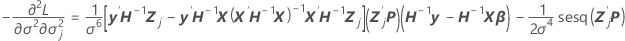

This component is also the value of the last column and the 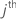 row by the symmetry property of the variance-covariance matrix.
row by the symmetry property of the variance-covariance matrix.

Notation
| Term | Description |
|---|---|
 | the trace of matrix  |
For further details on the notation, go to the Methods section.
