Sums of squares (SS) and standard deviations are closely related. Standard deviations are just sums of squares divided by the appropriate degrees of freedom.
In This Topic
SS Total
SS Total = SS Within + SS Between
SS Total is the sum of all squared deviations of individual observations from the overall process mean.
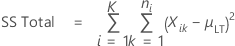
where:
- Xik = kth data of the ith subgroup
- μLT = overall process mean
SS Within
SS Within is the sum of all squared deviations of individual observations from their subgroup means.
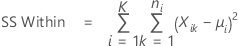
where:
- Xik = kth data of the ith subgroup
- μi = mean of ith subgroup
Thus, SS Within is purely a function of the inherent variation of the process. However, SS Between is a function of the natural variation in subgroup means and changes in subgroup means that are caused by shifts and drifts in the process mean.
SS Between
SS Between is the sum of squared deviations of subgroup means from the overall process mean.
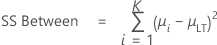
where:
- μi = mean of ith subgroup
- μLT = overall process mean
