In This Topic
- Cohen's kappa statistic (unknown standard)
- Cohen's kappa statistic (known standard)
- Testing significance of Cohen's kappa
- Fleiss' kappa statistic (unknown standard)
- Testing significance of Fleiss' kappa (unknown standard)
- Fleiss' kappa statistic (known standard)
- Test the significance of Fleiss' kappa (known standard)
Cohen's kappa statistic (unknown standard)
- Within appraiser — there are exactly two trials with an appraiser
- Between appraisers — there are exactly two appraisers each having one trial only
For a particular response value, kappa can be calculated by collapsing all responses that are not equal to the value in one category. Then, you can use the 2X2 table to calculate kappa.
Formulas
When the true standard is unknown, Minitab estimates Cohen's kappa by:

| Trial B (or Appraiser B) | |||||
| Trial A (or Appraiser A) | 1 | 2 | ... | k | Total |
| 1 | p11 | p12 | ... | p1k | p1+ |
| 2 | p21 | p22 | ... | p2k | P2+ |
| .... | |||||
| k | pk1 | pk2 | ... | pkk | pk+. |
| Total | p.+1 | p.+2 | ... | p.+k | 1 |
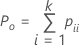
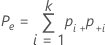
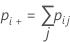
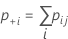

Notation
| Term | Description |
|---|---|
| Po | the observed proportion of agreement |
| pii | each value in the diagonal of the two-way table |
| Pe | the expected proportion of times k appraisers agree |
| nij | the number of samples in the ith row and the jth column |
| N | the total number of samples |
Cohen's kappa statistic (known standard)
Use Cohen's kappa statistic when classifications are nominal. When the standard is known and you choose to obtain Cohen's kappa, Minitab will calculate the statistic using the formulas below.
The kappa coefficient for the agreement of trials with the known standard is the mean of these kappa coefficients.
Formulas
When the true standard is known, first calculate kappa using the data from each trial and the known standard.

| Standard | |||||
| Trial A | 1 | 2 | ... | k | Total |
| 1 | p11 | p12 | ... | p1k | p1+ |
| 2 | p21 | p22 | ... | p2k | P2+ |
| .... | |||||
| k | pk1 | pk2 | ... | pkk | pk+. |
| Total | p.+1 | p.+2 | ... | p.+k | 1 |
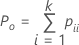
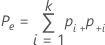
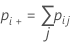
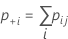

Notation
| Term | Description |
|---|---|
| Po | the observed proportion of agreement |
| pii | each value in the diagonal of the two-way table |
| Pe | the expected proportion of times k appraisers agree |
| nij | the number of samples in the ith row and the jth column |
| N | the total number of samples |
Testing significance of Cohen's kappa
To test the null hypothesis that the ratings are independent (so that kappa = 0), use:
z = kappa / SE of kappa
This is a one-sided test. Under the null hypothesis, z follows the standard normal distribution. Reject the hypothesis if z is significantly larger than the α critical value.
Formulas
The standard error of kappa for each trial and the standard is:
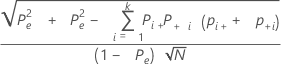
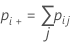
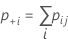
Notation
| Term | Description |
|---|---|
| Pe | the expected proportion of times k appraisers agree |
| N | the total number of samples |
Fleiss' kappa statistic (unknown standard)
- Case 1—Agreement within each appraiser
- Calculate the kappa coefficients that represent the agreement within each appraiser.
- Case 2—Agreement between all appraisers
- Calculate the kappa coefficients that represent the agreement between all appraisers.
Formulas for overall kappa
Define xij to be the number of ratings on sample i into category j, where i is from 1 to n, and j is from 1 to k.
The overall kappa coefficient is defined by:
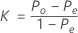
where:
Po is the observed proportion of the pairwise agreement among the m trials.
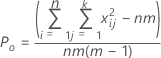
Pe is the expected proportion of agreement if the ratings from one trial is independent of another.
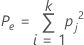
pj represents the overall proportion of ratings in category j.
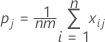
Substituting Po and Pe into K, the overall kappa coefficient is estimated by:
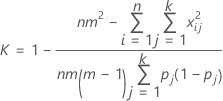
| Term | Description |
|---|---|
| k | the total number of categories |
| m | the number of trials—for case 1, m = the number of trials for each appraiser; for case 2, m = the number of trials for all appraisers. |
| n | the number of samples |
| xij | the number of ratings on sample i into category j |
Formulas for kappa for a single category
For measuring agreement with respect to classifications into a single one of the k categories, say the jth, one may combine all categories, other than the one of current interest, into a single category and apply the above equation. The resulting formula for the kappa statistic for the jth category is:
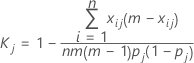
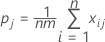
where:
| Term | Description |
|---|---|
| k | the total number of categories |
| m | the number of trials—for case 1, m = the number of trials for each appraiser; for case 2, m = the number of trials for all appraisers. |
| n | the number of samples |
| xij | the number of ratings on sample i into category j |
Testing significance of Fleiss' kappa (unknown standard)
The null hypothesis, H0, is kappa = 0. The alternative hypothesis, H1, is kappa > 0.
Under the null hypothesis, Z is approximately normally distributed and is used to calculate the p-values.
Formulas
To test whether kappa > 0, use the following Z statistic:

Var (K) is calculated by:
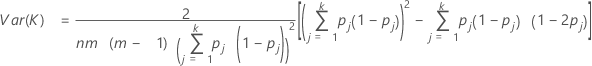
To test whether kappa > 0 for the jth category, use the following Z statistic:

Var (Kj) is calculated by:

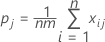
Notation
| Term | Description |
|---|---|
| K | the overall kappa statistic |
| Kj | the kappa statistic for the jth category |
| k | the total number of categories |
| m | the number of trials—for case 1, m = the number of trials for each appraiser; for case 2, m = the number of trials for all appraisers. |
| n | the number of samples |
| xij | the number of ratings on sample i into category j |
Fleiss' kappa statistic (known standard)
Use the following steps to calculate overall kappa and kappa for a specific category when the standard rating for each sample is known.
Assume there are m trials.
Note
See the formulas from Fleiss' kappa statistic (unknown standard).
- For each trial, calculate kappa using the ratings from the trial, and the ratings given by the standard. In other words, treat the standard as another trial, and use the unknown standard kappa formulas for two trials to estimate kappa.
- Repeat the calculation for all m trials. Now you have m overall kappa values and m kappa values for the specific category values.
The overall kappa with known standard is then equal to the average of all the m overall kappa values.
In the same way, the kappa for a specific category with known standard is the average of all the m kappa for specific category values.
Test the significance of Fleiss' kappa (known standard)
The null hypothesis, H0, is kappa = 0. The alternative hypothesis, H1, is kappa > 0.
Under the null hypothesis, Z is approximately normally distributed and is used to calculate the p-values.

Where K is the kappa statistic, Var(K) is the variance of the kappa statistic.
Note
See the formulas from Fleiss' kappa statistic (unknown standard)
Assume there are m trials.
- For each trial, calculate variance of kappa using the ratings from the trial, and the ratings given by the standard. In other words, treat the standard as the second trial, and use the variance of kappa formulas for two trial and unknown standard case to calculate the variance.
- Repeat the calculation for all m trials. Now you have m variances for overall kappa and m variances for kappa for specific categories.
The variance of overall kappa with known standards is then equal to the sum of the m variances for overall kappa divided by m2.
Similarly, the variance of kappa for a specific category with known standard equals the sum of the m variances for the kappa for a specific category divided by m2.
