Minitab®  Support

Example of Attribute Agreement Analysis

Learn more about Minitab

Fabric appraisers at a textile printing company rate the print quality of cotton fabric on a 1 to 5 point scale. The quality engineer wants to assess the consistency and correctness of the appraisers' ratings. The engineer asks four appraisers to rate print quality on 50 samples of fabric twice, in random order.

Because the data include a known standard for each sample, the quality engineer can assess the consistency and correctness of ratings compared to the standard as well as compared to other appraisers.

  1. Open the sample data, TextilePrintQuality.MTW.
  2. Choose Stat > Quality Tools > Attribute Agreement Analysis.
  3. In Data are arranged as, select Attribute column and enter Response.
  4. In Samples, enter Sample.
  5. In Appraisers, enter Appraiser.
  6. In Known standard/attribute, enter Standard.
  7. Select Categories of the attribute data are ordered.
  8. Click OK.

Interpret the results

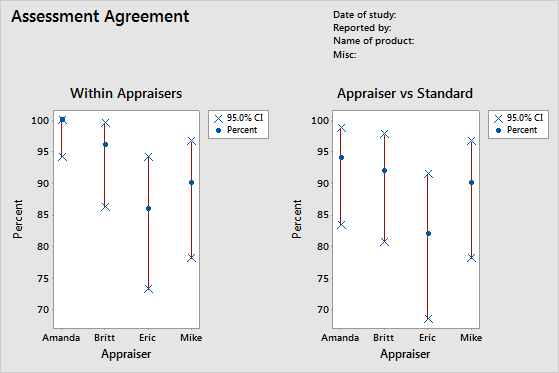
Within Appraisers table
Because each appraiser provides two or more ratings for each sample, the engineer can evaluate the consistency of each appraiser.
All of the appraisers have good match rates, from Amanda with 100% to Eric with 86%.
The p-value for Fleiss' kappa statistics is 0.0000 for all appraisers and all responses, with α = 0.05. Therefore, the engineer rejects the null hypothesis that the agreement is due to chance alone.
Because this example has ordinal ratings, the engineer examines Kendall's coefficient of concordance. The Kendall's coefficient of concordance for all appraisers ranges between 0.98446 and 1.000, which indicates a high level of agreement.
Each Appraiser vs Standard table
Because there is a known standard for each sample, the engineer can evaluate the accuracy and consistency of each of the appraiser's ratings.
Each appraiser rated 50 fabric samples (# Inspected). Amanda correctly judged 47 samples across trials (#Matched), for 94% matched. Eric correctly judged 41 samples across trials, for 82% matched.
The p-value for Fleiss' kappa is 0.0000 for all appraisers and all responses, with α = 0.05. Therefore, the engineer rejects the null hypothesis that the agreement is due to chance alone.
The Kendall's correlation coefficient for all appraisers ranges between 0.951863 and 0.975168, which confirms the high level of agreement with the standard.
Between Appraisers table
The Between Appraisers table shows that the appraisers agree on their ratings for 37 of the 50 samples.
The overall kappa value of 0.881705 indicates a good level of absolute agreement of the ratings between appraisers. The Kendall's coefficient of concordance of 0.976681 confirms this strong association.
The between-appraisers statistics do not compare the appraisers' ratings to the standard. Although the appraisers' ratings may be consistent, these statistics do not indicate whether the ratings are correct.
All Appraisers vs Standard table
Because there is a known standard for each sample, the engineer can evaluate the accuracy of all the appraisers' ratings.
The appraisers matched 37 of 50 ratings of all appraiser assessments with the known standard, for 74.0% matched.
The overall kappa value of 0.912082 indicates a good level of absolute agreement of the ratings between appraisers and with the standard. The Kendall's coefficient of concordance of 0.965563 confirms this strong association.
The all appraisers versus standard statistics do compare the appraisers' ratings to the standard. The engineer can conclude that the appraisers' ratings are consistent and correct.
Note

The p-value of 0.0000 in the output is rounded. But you can safely conclude that the p-value is very low and is < 0.00005.

Attribute Agreement Analysis for Response

Within Appraisers

Assessment Agreement Appraiser # Inspected # Matched Percent 95% CI Amanda 50 50 100.00 (94.18, 100.00) Britt 50 48 96.00 (86.29, 99.51) Eric 50 43 86.00 (73.26, 94.18) Mike 50 45 90.00 (78.19, 96.67) # Matched: Appraiser agrees with him/herself across trials.
Fleiss’ Kappa Statistics Appraiser Response Kappa SE Kappa Z P(vs > 0) Amanda 1 1.00000 0.141421 7.0711 0.0000 2 1.00000 0.141421 7.0711 0.0000 3 1.00000 0.141421 7.0711 0.0000 4 1.00000 0.141421 7.0711 0.0000 5 1.00000 0.141421 7.0711 0.0000 Overall 1.00000 0.071052 14.0741 0.0000 Britt 1 1.00000 0.141421 7.0711 0.0000 2 0.89605 0.141421 6.3360 0.0000 3 0.86450 0.141421 6.1129 0.0000 4 1.00000 0.141421 7.0711 0.0000 5 1.00000 0.141421 7.0711 0.0000 Overall 0.94965 0.071401 13.3002 0.0000 Eric 1 0.83060 0.141421 5.8733 0.0000 2 0.84000 0.141421 5.9397 0.0000 3 0.70238 0.141421 4.9666 0.0000 4 0.70238 0.141421 4.9666 0.0000 5 1.00000 0.141421 7.0711 0.0000 Overall 0.82354 0.071591 11.5034 0.0000 Mike 1 1.00000 0.141421 7.0711 0.0000 2 0.83060 0.141421 5.8733 0.0000 3 0.81917 0.141421 5.7924 0.0000 4 0.86450 0.141421 6.1129 0.0000 5 0.86450 0.141421 6.1129 0.0000 Overall 0.87472 0.070945 12.3295 0.0000
Kendall’s Coefficient of Concordance Appraiser Coef Chi - Sq DF P Amanda 1.00000 98.0000 49 0.0000 Britt 0.99448 97.4587 49 0.0000 Eric 0.98446 96.4769 49 0.0001 Mike 0.98700 96.7256 49 0.0001

Each Appraiser vs Standard

Assessment Agreement Appraiser # Inspected # Matched Percent 95% CI Amanda 50 47 94.00 (83.45, 98.75) Britt 50 46 92.00 (80.77, 97.78) Eric 50 41 82.00 (68.56, 91.42) Mike 50 45 90.00 (78.19, 96.67) # Matched: Appraiser’s assessment across trials agrees with the known standard.
Fleiss’ Kappa Statistics Appraiser Response Kappa SE Kappa Z P(vs > 0) Amanda 1 1.00000 0.100000 10.0000 0.0000 2 0.83060 0.100000 8.3060 0.0000 3 0.81917 0.100000 8.1917 0.0000 4 1.00000 0.100000 10.0000 0.0000 5 1.00000 0.100000 10.0000 0.0000 Overall 0.92476 0.050257 18.4006 0.0000 Britt 1 1.00000 0.100000 10.0000 0.0000 2 0.83838 0.100000 8.3838 0.0000 3 0.80725 0.100000 8.0725 0.0000 4 1.00000 0.100000 10.0000 0.0000 5 1.00000 0.100000 10.0000 0.0000 Overall 0.92462 0.050396 18.3473 0.0000 Eric 1 0.91159 0.100000 9.1159 0.0000 2 0.81035 0.100000 8.1035 0.0000 3 0.72619 0.100000 7.2619 0.0000 4 0.84919 0.100000 8.4919 0.0000 5 1.00000 0.100000 10.0000 0.0000 Overall 0.86163 0.050500 17.0622 0.0000 Mike 1 1.00000 0.100000 10.0000 0.0000 2 0.91694 0.100000 9.1694 0.0000 3 0.90736 0.100000 9.0736 0.0000 4 0.92913 0.100000 9.2913 0.0000 5 0.93502 0.100000 9.3502 0.0000 Overall 0.93732 0.050211 18.6674 0.0000
Kendall’s Correlation Coefficient Appraiser Coef SE Coef Z P Amanda 0.967386 0.0690066 14.0128 0.0000 Britt 0.967835 0.0690066 14.0193 0.0000 Eric 0.951863 0.0690066 13.7879 0.0000 Mike 0.975168 0.0690066 14.1256 0.0000

Between Appraisers

Assessment Agreement # Inspected # Matched Percent 95% CI 50 37 74.00 (59.66, 85.37) # Matched: All appraisers’ assessments agree with each other.
Fleiss’ Kappa Statistics Response Kappa SE Kappa Z P(vs > 0) 1 0.954392 0.0267261 35.7101 0.0000 2 0.827694 0.0267261 30.9695 0.0000 3 0.772541 0.0267261 28.9058 0.0000 4 0.891127 0.0267261 33.3429 0.0000 5 0.968148 0.0267261 36.2248 0.0000 Overall 0.881705 0.0134362 65.6218 0.0000
Kendall’s Coefficient of Concordance Coef Chi - Sq DF P 0.976681 382.859 49 0.0000

All Appraisers vs Standard

Assessment Agreement # Inspected # Matched Percent 95% CI 50 37 74.00 (59.66, 85.37) # Matched: All appraisers’ assessments agree with the known standard.
Fleiss’ Kappa Statistics Response Kappa SE Kappa Z P(vs > 0) 1 0.977897 0.0500000 19.5579 0.0000 2 0.849068 0.0500000 16.9814 0.0000 3 0.814992 0.0500000 16.2998 0.0000 4 0.944580 0.0500000 18.8916 0.0000 5 0.983756 0.0500000 19.6751 0.0000 Overall 0.912082 0.0251705 36.2362 0.0000
Kendall’s Correlation Coefficient Coef SE Coef Z P 0.965563 0.0345033 27.9817 0.0000
Copyright © 2024 Minitab, LLC. All rights Reserved.