Methods and formulas for U Chart Diagnostic

Select the method or formula of your choice.

In This Topic

Plotted points
Ratio of observed variation to expected variation
95% confidence limits for ratio
Decision

Plotted points

Adjusted counts

Minitab calculates the adjusted defect counts (a_i) as follows:

Transformed counts

The adjusted counts are then transformed using the following formula:

Then Minitab creates a standard normal probability plot of the transformed counts using the method specified in File > Options > Individual Graphs > Probability Plots.

Notation

Term	Description
d_i	defect count for subgroup i
n_i	size of subgroup i
	average subgroup size

Ratio of observed variation to expected variation

Expected variation

The expected variation is equal to the standard deviation of the transformed counts (X_i), which is equal to 1.

Observed variation

To calculate the observed variation, Minitab calculates normal scores (Y,) for the transformed counts as follows:

where NSCOR is the Normal scores function (available by choosing Calc > Calculator).

For the next step, only the middle 50% of the X_i values are used, along with their corresponding Y_i values. X_i values are excluded if they are less than the 25^th percentile or greater than the 75^th percentile.

Minitab fits a least squares regression model with Y_i as the response and X_i as the predictor:

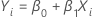
The observed variation is then 1 / β₁.

Ratio

The ratio of observed variation to expected variation is calculated as follows:

Notation

Term	Description
X_i	transformed counts (For more information, see the section "Plotted points".)
β₀	intercept from the least squares regression equation
β₁	slope coefficient from the least squares regression equation

95% confidence limits for ratio

upper confidence limit

The upper confidence limit for the ratio is calculated as follows:

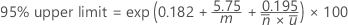
where 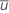is the mean defect rate, calculated as follows:

lower confidence limit

For the lower confidence limit for the ratio, Minitab uses a conservative, fixed value of 60%.

Notation

Term	Description
m	number of subgroups
	average subgroup size
d_i	defect count for subgroup i
n_i	size of subgroup i

Decision

Minitab compares the ratio of observed variation to expected variation to the 95% upper confidence limit and the 95% lower confidence limit.

If ratio > upper confidence limit: If the ratio is greater than the upper confidence limit, then using a traditional U chart with the data may result in an elevated false alarm rate. A Laney U' chart is recommended.
If ratio < lower confidence limit: If the ratio is less than the lower confidence limit, then using a traditional U chart with the data may result in control limits that are too wide. A Laney U' chart is recommended.