In This Topic
StDev (Within)
Within standard deviation is an estimate of the variation within the subgroups. If your data are collected properly, the within-subgroup variation should not be influenced by changes to process inputs, such as tool wear or different lots of material. In that case, the within standard deviation represents the natural and inherent variation of the process over a short period of time. It indicates the potential variation of the process if shifts and drifts between subgroups were eliminated.
Note
If you use a data transformation when you perform the capability analysis, Minitab also calculates StDev(Within)*, the within-subgroup standard deviation of the transformed data.
Interpretation
Compare the within-subgroup standard deviation with the overall standard deviation. A substantial difference between the within-subgroup standard deviation and the overall standard deviation may indicate that the process is not stable, or that your process has other sources of variation in addition to the variation within subgroups. Use a control chart to verify that your process is stable before you perform a capability analysis.
Minitab uses the within-subgroup standard deviation to calculate Cp, Cpk, and other measures of the potential capability of your process.
Cp
- The specification spread (USL – LSL)
- The spread of the process (the 6-σ variation) based on the within-subgroup standard deviation
Interpretation
Use Cp to evaluate the potential capability of your process based on the process spread. Potential capability indicates the capability that could be achieved if process shifts and drifts were eliminated.
Because Cp does not consider the location of the process, it indicates the potential capability that your process could achieve if it were centered. Generally, higher Cp values indicate a more capable process. Lower Cp values indicate that your process may need improvement.
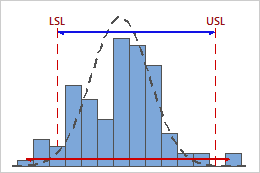
Low Cp
In this example, the specification spread is less than the within-subgroup process spread. Therefore, Cp is low (0.80), and the potential capability of the process is poor based on its variability.
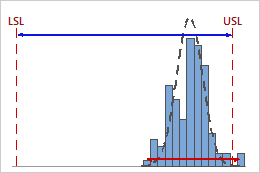
High Cp
In this example, the specification spread is considerably greater than the within-subgroup process spread. Therefore, Cp is high (2.76), and the potential capability of the process is good based on its variability.
-
Compare Cp to a benchmark value to assess the potential capability of your process. Many industries use a benchmark value of 1.33. If Cp is lower than your benchmark, consider how to improve your process by reducing its variation.
-
Compare Cp and Cpk. If Cp and Cpk are approximately equal, then the process is centered between the specification limits. If Cp and Cpk differ, then the process is not centered.
Caution
Because the Cp index does not consider the process location, it does not indicate how close the process is to the target region that is defined by the specification limits. For example, the following graphs show two processes with the same Cp value, yet one process falls within the specification limits and the other does not.
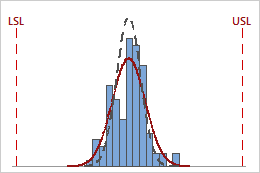
Cp = 3.13
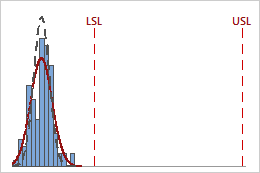
Cp = 3.13
For a complete and accurate analysis, use graphs in combination with other capability indices (such as Cpk) to draw meaningful conclusions from your data.
Cpk
- The distance from the process mean to the closest specification limit (USL or LSL)
- The one-sided spread of the process (the 3-σ variation) based on the within-subgroup standard deviation
Interpretation
Use Cpk to evaluate the potential capability of your process based on both the process location and the process spread. Potential capability indicates the capability that could be achieved if process shifts and drifts were eliminated.
Generally, higher Cpk values indicate a more capable process. Lower Cpk values indicate that your process may need improvement.
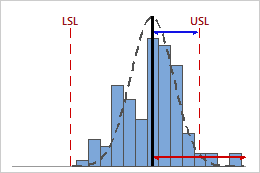
Low Cpk
In this example, the distance from the process mean to the nearest specification limit (USL) is less than the one-sided process spread. Therefore, Cpk is low (0.80), and the potential capability of the process is poor.
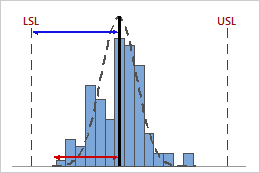
High Cpk
In this example, the distance from the process mean to the nearest specification limit (LSL) is greater than the one-sided process spread. Therefore, Cpk is high (1.64), and the potential capability of the process is good.
You can compare Cpk with other values to get more information about the capability of your process.
-
Compare Cpk with a benchmark that represents the minimum value that is acceptable for your process. Many industries use a benchmark value of 1.33. If Cpk is lower than your benchmark, consider ways to improve your process, such as reducing its variation or shifting its location.
-
Compare Cp and Cpk. If Cp and Cpk are approximately equal, then the process is centered between the specification limits. If Cp and Cpk differ, then the process is not centered.
-
Compare Ppk and Cpk. When a process is in statistical control, Ppk and Cpk are approximately equal. The difference between Ppk and Cpk represents the improvement in process capability that you could expect if shifts and drifts in the process were eliminated.
Caution
The Cpk index represents only one side of the process curve, and does not measure how the process performs on the other side of the process curve.
For example, the following graphs display two processes with identical Cpk values. However, one process violates both specification limits, and the other process only violates the upper specification limit.
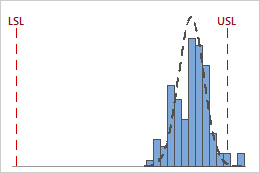
Cpk = min {CPL = 4.58, CPU = 0.93} = 0.93
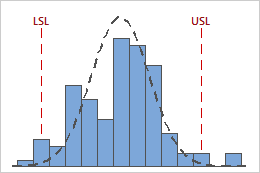
Cpk = CPL = CPU = 0.93
If your process has nonconforming parts that fall on both sides of the specification limits, consider using other indices to more fully assess process capability.
PPM Total for Expected Within Performance
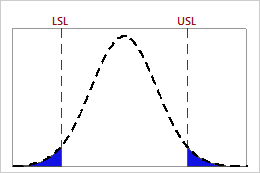
Interpretation
Use PPM Total for expected within performance to estimate the number of nonconforming items, represented in parts per million, that you can expect to be outside the specification limits based on the variation within the subgroups. Within performance values indicate the potential performance that your process could achieve if shifts and drifts were eliminated.
Lower values of PPM Total indicate greater process capability. Ideally, few or no parts have measurements that are outside the specification limits.
| PPM | % Nonconforming Parts | % Conforming |
|---|---|---|
| 66807 | 6.6807% | 93.3193% |
| 6210 | 0.621% | 99.379% |
| 233 | 0.0233% | 99.9767% |
| 3.4 | 0.00034% | 99.99966% |
Z.Bench for Potential (Within) Capability
Z.bench (within) is the percentile on a standard normal distribution that translates the estimated probability of defects in the process to an upper tail probability. It is calculated based on the potential (within) process performance, using the within-subgroup standard deviation.
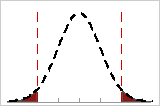
The defects for the process fall on both sides of the specification limits. The within-subgroup standard deviations are shown by the tick marks.
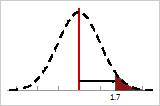
If you put all the defects on the right tail of the distribution, and then measure the number of within-subgroup standard deviations from the center (vertical line) to the point that defines the total defects, you obtain the Z-bench (within) value.
Note
To display Z.bench measures, you must click Options and change the default output from capability statistics to benchmark Z's when you perform the capability analysis.
Interpretation
Use Z.Bench (within) to evaluate the potential sigma capability of your process. Potential capability indicates the capability that could be achieved if process shifts and drifts were eliminated.
Generally, higher Z.bench (within) values indicate that the process is more capable. Lower values indicate that your process may need improvement. When possible, compare Z.bench (within) with a benchmark value based on process knowledge or industry standards. If Z.bench (within) is less than your benchmark, consider ways to improve your process.
Compare Z.Bench (within) and Z.Bench (overall). When a process is in statistical control, Z.Bench (within) and Z.Bench (overall) are approximately equal. The difference between the two values represents the improvement in process capability that you could expect if the process were brought into control. Zbench (Within) is sometimes referred to as Z.Bench Short-Term (ST).
