In This Topic
Estimating standard deviation
Between/within capability analysis is based on the following four standard deviations:
Within-subgroup standard deviation
σwithin is an estimate of the variation within subgroups (for example, one shift, one operator, or one material batch). Minitab estimates σwithin using one of the following methods:
- Pooled standard deviation:

where:
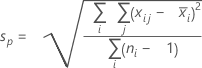
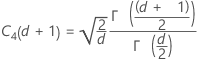
Note
If you change the default method and choose not to use the unbiasing constant, σwithin is estimated by Sp.
Term Description d Degrees of freedom for Sp= Σ (ni- 1) Xij jth observation in the ith subgroup X̅i Mean of the ith subgroup ni Number of observations in the ith subgroup C4(d+1) Unbiasing constant Γ(·) Gamma function - Average of subgroup ranges
(Rbar):

where:
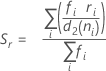
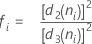
If n are all the same:
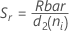
Term Description ri Range of the ith subgroup d2 (ni) An unbiasing constant read from a table (for more information, see the section Unbiasing constants d2(), d3(), and d4() d3 (ni) An unbiasing constant read from a table (for more information, see the section Unbiasing constants d2(), d3(), and d4() ni Number of observations in the ith subgroup - Average of subgroup standard
deviations (Sbar):

where:
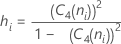
Note
If you change the default setting and do not use the unbiasing constant, σwithin is estimated by Σ Si / number of subgroups.
Term Description C4(ni) Unbiasing constant (as defined for pooled standard deviation) Si Standard deviation of subgroup i ni Number of observations in the ith subgroup
Between-subgroup standard deviation
σBetween is an estimate of the variation between subgroups (for example, subgroups collected at set intervals, batches, or by different operators).

- Average of moving range:

where:

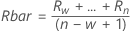
Term Description Ri The ith moving range w The number of observations used in the moving range. The default is w = 2. d2(w) An unbiasing constant read from a table (for more information, see the section Unbiasing constants d2(), d3(), and d4() - Median of moving range:

where:

Term Description MRi The ith moving range 
Median of the MRi w The number of observations used in the moving range. The default is w = 2. d4(w) An unbiasing constant read from a table (for more information, see the section Unbiasing constants d2(), d3(), and d4() - Square root of mean squared
successive differences (MSSD):
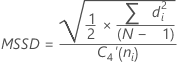
Note
If you change the default setting and do not use the unbiasing constant, σwithin is estimated by

Term Description di Differences of successive group means C4(ni) Unbiasing constant (as defined for the pooled standard deviation) C4'(ni) Unbiasing constant ≈ c4(ni). For more information, see the section Unbiasing constant c4'(). N Total number of observations ni Number of observations in the ith subgroup
Between/within standard deviation

| Term | Description |
|---|---|
| σ2Between | Variance between subgroups |
| σ2within | Variance within subgroups |
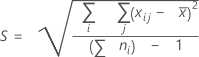
Overall standard deviation

where:
Note
By default, Minitab does not use the unbiasing constant when estimating σoverall. σoverall is estimated by S. If you want to estimate overall standard deviation using the unbiasing constant, you can change this option on the Estimate subdialog box when you perform the capability analysis. If you always want Minitab to use the unbiasing constant by default, choose and select the appropriate options.
| Term | Description |
|---|---|
| Xij | The jth observation in the ith subgroup |
| X̅ | Process mean |
| ni | Number of observations in the ith subgroup |
| C4 (N) | Unbiasing constant (as defined for the pooled standard deviation) |
| N (or Σ ni) | Total number of observations |
Box-Cox transformation
The Box-Cox transformation estimates a lambda value, as shown in the following table, which minimizes the standard deviation of a standardized transformed variable. The resulting transformation is Yλ when λ ҂ 0 and ln Y when λ = 0.
The Box-Cox method searches through many types of transformations. The following table shows some common transformations where Y' is the transform of the data Y.
| Lambda (λ) value | Transformation |
|---|---|
 |
 |
 |
 |
 |
 |
 |
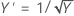 |
 |
 |
