Example of creating a variables acceptance sampling plan

A manufacturing engineer receives weekly shipments of 2-inch plastic pipe segments for an assembly process. The lot size is 2500.

The engineer decides to implement a sampling plan to verify the pipe wall thickness. The lower specification for the pipe wall thickness is 0.09 inches. The engineer and the supplier agree that the AQL is 100 defectives per million and the RQL is 300 defectives per million.

Choose Stat > Quality Tools > Acceptance Sampling by Variables > Create/Compare.
From the drop-down list, select Create a Sampling Plan.
In Units for quality levels, select Defectives per million.
In Acceptable quality level (AQL), enter 100.
In Rejectable quality level (RQL or LTPD), enter 300.
In Producer’s risk (Alpha), enter 0.05.
In Consumer’s risk (Beta), enter 0.10.
In Lower spec, enter 0.09.
In Historical standard deviation, enter 0.025.
In Lot size, enter 2500.
Click OK.

Interpret the results

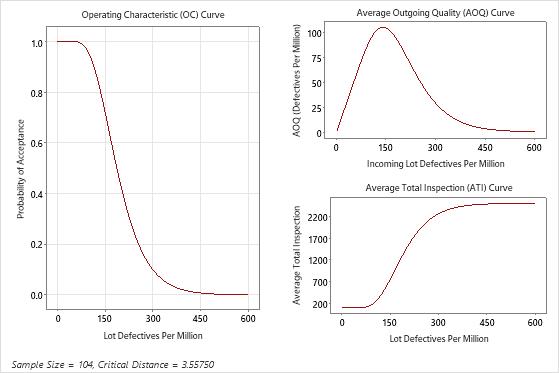
For each lot of 2500 pipe segments, the engineer should randomly select and measure the thickness of 104 pipes.

If Z.LSL is greater than the critical distance, in this case k = 3.55750, the engineer accepts the entire lot. Otherwise, the engineer rejects the entire lot.

In this case, the probability of acceptance at the AQL (100 defectives per million) is 0.95, and the probability of rejecting is 0.05. The engineer and the supplier agreed that lots of 100 defectives per million would be accepted approximately 95% of the time to protect the producer. The probability of accepting at the RQL (300 defectives per million) is 0.10, and the probability of rejecting is 0.90. The engineer and the supplier agreed that lots of 300 defectives per million would be rejected most of the time to protect the consumer.

When entire lots are rejected, they are usually subjected to 100% inspection, with defective items replaced or reworked. This type of inspection is called rectifying inspection. Use the following metrics to understand the impact of 100% inspection and rework:

The average outgoing quality (AOQ) represents the average quality of the lot after additional inspection and rework. The AOQ level is 91.1 defectives per million at the AQL and 28.6 defectives per million at the RQL. The average outgoing quality limit (AOQL) = 104.6 at 140 defectives per million and represents the worse case outgoing quality level.
The average total inspection (ATI) represents the average number of inspected items after additional inspection and rework. The ATI per lot represents the average number of pipes inspected at a particular quality level and probability of acceptance. For the quality level of 100 defectives per million, the average total number of pipes inspected per lot is 223.2. For the quality level of 300 defectives per million, the average total number of pipes inspected per lot is 2261.4.

Lot quality in defectives per million

Method

Lower Specification Limit (LSL)	0.09
Historical Standard Deviation	0.025
Lot Size	2500

Acceptable Quality Level (AQL)	100
Producer’s Risk (α)	0.05

Rejectable Quality Level (RQL or LTPD)	300
Consumer’s Risk (β)	0.1

Generated Plan(s)

Sample Size	104
Critical Distance (k Value)	3.55750

Defectives Per Million	Probability Accepting	Probability Rejecting	AOQ	ATI
100	0.950	0.050	91.1	223.2
300	0.100	0.900	28.6	2261.4

Average Outgoing Quality Limit(s) (AOQL)

AOQL	At Defectives per Million
104.6	140.0