N
The sample size (N) is the total number of observations in the original sample. Minitab takes resamples of this sample size to form the bootstrap samples.
Mean
The mean is the average of the data, which is the sum of all the observations divided by the number of observations.
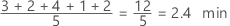
Interpretation
Use the mean to describe the sample with a single value that represents the center of the data. Many statistical analyses use the mean as a standard measure of the center of the distribution of the data.
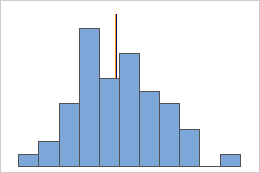
Symmetric
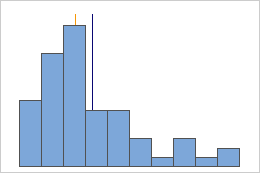
Not symmetric
For the symmetric distribution, the mean (blue line) and median (orange line) are so similar that you can't easily see both lines. But the non-symmetric distribution is skewed to the right.
StDev
The standard deviation is the most common measure of dispersion, or how spread out the data are about the mean. The symbol σ (sigma) is often used to represent the standard deviation of a population, while s is used to represent the standard deviation of a sample. Variation that is random or natural to a process is often referred to as noise.
Because the standard deviation is in the same units as the data, it is usually easier to interpret than the variance.
Interpretation
Use the standard deviation to determine how spread out the data are from the mean. A higher standard deviation value indicates greater spread in the data. A good rule of thumb for a normal distribution is that approximately 68% of the values fall within one standard deviation of the mean, 95% of the values fall within two standard deviations, and 99.7% of the values fall within three standard deviations.
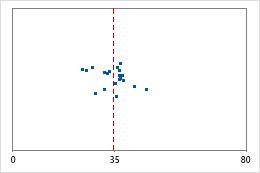
Hospital 1
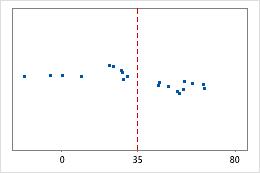
Hospital 2
Hospital discharge times
Administrators track the discharge time for patients who are treated in the emergency departments of two hospitals. Although the average discharge times are about the same (35 minutes), the standard deviations are significantly different. The standard deviation for hospital 1 is about 6. On average, a patient's discharge time deviates from the mean (dashed line) by about 6 minutes. The standard deviation for hospital 2 is about 20. On average, a patient's discharge time deviates from the mean (dashed line) by about 20 minutes.
Variance
The variance measures how spread out the data are about their mean. The variance is equal to the standard deviation squared.
Interpretation
The greater the variance, the greater the spread in the data.
Because variance (σ2) is a squared quantity, its units are also squared, which may make the variance difficult to use in practice. The standard deviation is usually easier to interpret because it's in the same units as the data. For example, a sample of waiting times at a bus stop may have a mean of 15 minutes and a variance of 9 minutes2. Because the variance is not in the same units as the data, the variance is often displayed with its square root, the standard deviation. A variance of 9 minutes2 is equivalent to a standard deviation of 3 minutes.
Minimum
The minimum is the smallest data value.
In these data, the minimum is 7.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretation
Use the minimum to identify a possible outlier or a data-entry error. One of the simplest ways to assess the spread of your data is to compare the minimum and maximum. If the minimum value is very low, even when you consider the center, the spread, and the shape of the data, investigate the cause of the extreme value.
Median
The median is the midpoint of the data set. This midpoint value is the point at which half the observations are above the value and half the observations are below the value. The median is determined by ranking the observations and finding the observation that are at the number [N + 1] / 2 in the ranked order. If the number of observations are even, then the median is the average value of the observations that are ranked at numbers N / 2 and [N / 2] + 1.
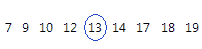
For this ordered data, the median is 13. That is, half the values are less than or equal to 13, and half the values are greater than or equal to 13. If you add another observation equal to 20, the median is 13.5, which is the average between 5th observation (13) and the 6th observation (14).
Interpretation

Symmetric

Not symmetric
For the symmetric distribution, the mean (blue line) and median (orange line) are so similar that you can't easily see both lines. But the non-symmetric distribution is skewed to the right.
Maximum
The maximum is the largest data value.
In these data, the maximum is 19.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretation
Use the maximum to identify a possible outlier or a data-entry error. One of the simplest ways to assess the spread of your data is to compare the minimum and maximum. If the maximum value is very high, even when you consider the center, the spread, and the shape of the data, investigate the cause of the extreme value.
Difference in Observed Means
Minitab indicates which population mean is subtracted from the other. The difference is the difference between the means of the two samples. This difference in observed means is an estimate of the difference in population means. To estimate a confidence interval for the difference in means of two independent groups, use Bootstrapping for 2-sample means.
