In This Topic
Histogram
A histogram divides sample values into many intervals and represents the frequency of data values in each interval with a bar.
Interpretation
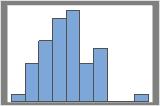
50 resamples
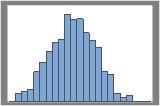
1000 resamples
The distribution is usually easier to determine with more resamples. For example, in these data, the distribution is ambiguous for 50 resamples. With 1000 resamples, the shape looks approximately normal.
The histogram visually shows the results of the hypothesis test. Minitab adjusts the data so that the center of the resamples is the same as the hypothesized mean. For a one-sided test, a reference line is drawn at the mean of the original sample. For a two-sided test, a reference line is drawn at the mean of the original sample and at the same distance on the opposite side of the hypothesized mean. The p-value is the proportion of sample means that are more extreme than the values at the reference lines. In other words, the p-value is the proportion of sample means that are as extreme as your original sample when you assume that the null hypothesis is true. These means are colored red on the histogram.
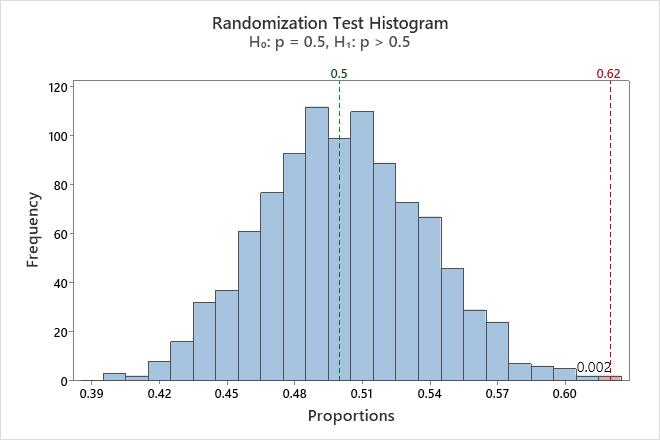
In this histogram, the bootstrap distribution appears to be normal. The p-value of 0.002 indicates that 0.2% of the sample proportions are greater than the proportion of the original sample.
Bar chart
The bar chart shows the proportion of occurrences for each category.
Note
Minitab displays a bar chart when you take only one resample. Minitab displays both the original data and the resample data.
Interpretation
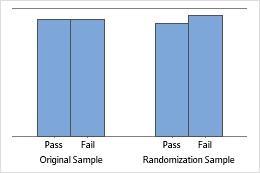
Sample proportion equals hypothesized proportion
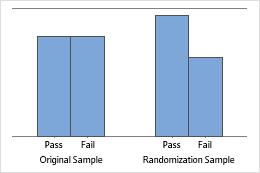
Sample proportion 20% less than hypothesized proportion
Proportion
The sample proportion equals the number of events divided by the sample size (N).
Interpretation
Minitab displays two different proportion values, the proportion of the observed sample and the proportion of the bootstrap distribution (Average). The proportion of the observed sample is an estimate of the population proportion. The proportion of the bootstrap distribution is usually close to the hypothesized proportion. The larger the difference between these two values, the more evidence you would expect against the null hypothesis.
Null hypothesis and alternative hypothesis
- Null hypothesis
- The null hypothesis states that a population parameter (such as the mean, the standard deviation, and so on) is equal to a hypothesized value. The null hypothesis is often an initial claim that is based on previous analyses or specialized knowledge.
- Alternative hypothesis
- The alternative hypothesis states that a population parameter is smaller, greater, or different than the hypothesized value in the null hypothesis. The alternative hypothesis is what you might believe to be true or hope to prove true.
Interpretation
In the output, the null and alternative hypotheses help you to verify that you entered the correct value for the hypothesized proportion.
Observed Sample
| N | Proportion |
|---|---|
| 200 | 0.620000 |
Randomization Test
| Null hypothesis | H₀: p = 0.5 |
|---|---|
| Alternative hypothesis | H₁: p > 0.5 |
| Number of Resamples | Average | P-Value |
|---|---|---|
| 1000 | 0.49942 | 0.002 |
In these results, the null hypothesis is that the population proportion is equal to 0.5. The alternative hypothesis is that the proportion is greater than 0.5.
Number of Resamples
The number of resamples is the number of times Minitab takes a random sample with replacement from your original data set. Usually, a large number of resamples works best.
Minitab adjusts the data so that the center of the resamples is the same as the hypothesized proportion. The sample size for each resample is equal to the sample size of the original data set. The number of resamples equals the number of observations on the histogram.
Average
The average is the sum of the proportions in the bootstrapping sample divided by the number of resamples. Minitab adjusts the data so that the center of the resamples is the same as the hypothesized proportion.
Interpretation
Minitab displays two different proportion values, the proportion of the observed sample and the proportion of the bootstrap distribution (Average). The proportion of the observed sample is an estimate of the population proportion. The proportion of the bootstrap distribution is usually close to the hypothesized proportion. The larger the difference between these two values, the more evidence you would expect against the null hypothesis.
P-Value
The p-value is the proportion of sample proportions that are as extreme as your original sample when you assume that the null hypothesis is true. A smaller p-value provides stronger evidence against the null hypothesis.
Interpretation
Use the p-value to determine whether the population proportion is statistically different from the hypothesized proportion.
- P-value ≤ α: The difference between the proportions is statistically significant (Reject H0)
- If the p-value is less than or equal to the significance level, the decision is to reject the null hypothesis. You can conclude that the difference between the population proportion and the hypothesized proportion is statistically significant. To calculate a confidence interval and determine whether the difference is practically significant, use Bootstrapping for 1-sample function. For more information, go to Statistical and practical significance.
- P-value > α: The difference between the proportions is not statistically significant (Fail to reject H0)
- If the p-value is greater than the significance level, the decision is to fail to reject the null hypothesis. You do not have enough evidence to conclude that the difference between the population proportion and the hypothesized proportion is statistically significant.
