By default, the bottom of the box is at the 1st quartile (Q1), and the top is at the 3rd quartile (Q3) value. The whiskers are the lines that extend from the top and bottom of the box to the adjacent values. The adjacent values are the lowest and highest observations that are still inside the region defined by the following limits:
- Lower Limit: Q1 - 1.5 (Q3 - Q1)
- Upper Limit: Q3 + 1.5 (Q3 - Q1)
However, the upper adjacent value can be less than Q3, which forces the whisker to be drawn from Q3 into the box. The lower adjacent value can also be greater than Q1, which forces the whisker to be drawn from Q1 into the box.
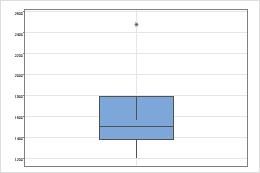
Example of a boxplot with an "ingrown" whisker
This boxplot shows the following data: 1200 1443 1490 1528 1563 2479.
For this boxplot:
- Q1 = 1382
- Q3 = 1792
- Lower Limit = 1382 - 1.5*(1792-1382) = 767
- Upper Limit = 1792 + 1.5*(1792-1382) = 2407
The smallest observation within this range is 1200 and the largest is 1563. The lower whisker connects Q1=1382 to 1200, which extends out of the box. The upper whiskers connects Q3=1792 to 1536, which extends into the box.
Note
If you choose to use hinges instead of quartiles for the box end points, whiskers will never be "ingrown".
