Select the method or formula of your choice.
In This Topic
- General formulas for sample size for tolerance intervals
- Calculating sample size for normal tolerances intervals
- Calculating maximum percentage of population in interval for normal tolerances intervals
- Calculating sample size and maximum acceptable percentages of population for interval for nonparametric tolerance intervals
General formulas for sample size for tolerance intervals
Definition of a tolerance interval (two-sided)
Let X1, X2, ..., Xn be the ordered values of a random sample of size n from some continuous distribution.Let the distribution function be F(χ,θ) for Ω in some parameter space with dimension greater than or equal to 1.
Let L < U be two statistics based on the sample such that for any given values α and P, with 0 < α < 1 and 0 < P < 1, the following holds for every θ in Ω:
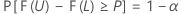
Then, the interval [ L, U] is a two-sided tolerance interval with content = P x 100% and confidence level = 100(1 - α)%. Such an interval can be called a two-sided (1 - α, P) tolerance interval. For example, if α = 0.10 and P = 0.85, then the resulting interval is called a two-sided (90% , 0.85) tolerance interval.
Sample size and margin of error
Let C = F( U) – F( L). A two-sided (1 –α , P) tolerance interval is such that: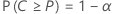
- The probability that the interval will cover at least 100P% of the population is 1 – α.
- The probability, α*, is small that the interval will cover more than 100P* % of the population, where P* = P + ε and ε > 0.
In other words, for given values of P, α, ε, and α*, the sample size is determined such that
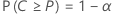
and

This approach is based on the fact that for any P* > P, P( C>P*) is a decreasing function of the sample size and therefore can be used to assess precision.
Choosing a small ε and α* has the effect of reducing the size of the tolerance interval, and thus a larger sample size is required. Typical values of ε and α* are 0.10, 0.05, or 0.01.
Note
The definitions and concepts above also apply to one-sided tolerance intervals.
- Faulkenberry, G.D. and Weeks, D.L. (1968). Sample size determination for tolerance limits. Technometrics, 10, 343-8.
Calculating sample size for normal tolerances intervals
One-sided interval
Faulkenberry and Daly1 show that for given values of α, P, ε , and α*, the required sample size for a one-sided interval is obtained by finding the minimum for n that satisfies the following equation:

where the notation tx,y(d) represents the yth percentile of a noncentral t-distribution with x degrees of freedom and noncentrality parameter d. The noncentrality parameters δ and δ* are calculated as follows:

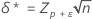
where zp is the Pth percentile of the standard normal distribution.
Minitab uses an iterative algorithm to find the required minimum value for n.
Two-sided interval
For the calculations for the sample size of a two-sided interval rely on the function I( k, n, P), go to Methods and formulas for Tolerance Intervals (Normal Distribution) and click "Exact tolerance intervals for normal distributions".
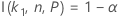
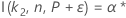
Minitab uses an iterative algorithm to find the required minimum value for n. For additional information, see Odeh, Chou, and Owen2.
Notation
| Term | Description |
|---|---|
| 1 – α | the confidence level of the tolerance interval |
| P | the coverage of the tolerance interval (the target minimum percentage of population in the interval) |
| ε | the margin of error of the tolerance interval |
| α* | the margin of error probability for the tolerance interval |
| n | the number of observations in the sample |
- Faulkenberry, G.D. and Daly, J.C. (1970). Sample size for tolerance limits on a normal distribution. Technometrics, 12, 813–21.
- Odeh, R. E., Chou, Y.-M. and Owen, D.B. (1987). The precision for coverages and sample size requirements for normal tolerance intervals. Communications in Statistics: Simulation and Computation, 16, 969–985.
Calculating maximum percentage of population in interval for normal tolerances intervals
P* = P + ε
The calculations for the margin of error are similar to the sample size calculations described in General formulas for sample size for tolerance intervals.
One-sided intervals
For given values of n, α, P, and α *, the margin of error, ε, for a one-sided interval is obtained by first solving for δ* in the following equation:
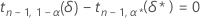
where the notation tx,y(d) represents the yth percentile of a noncentral t-distribution with x degrees of freedom and noncentrality parameter d. Minitab uses a numerical root finder routine to calculate δ*. With the value of δ* determined, the value of ε can be obtained from the following formula:

Two-sided intervals
The calculations for the margin of error of a two-sided interval rely on the function I( k, n, P), which is described in Exact tolerance intervals for normal distributions.
For given values of n, α, P, and α*, the margin of error, ε, for a two-sided interval is obtained using the algorithm described in Odeh, Chou, and Owen1. First, solve the following equation for k:
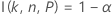

Notation
| Term | Description |
|---|---|
| 1 – α | the confidence level of the tolerance interval |
| P | the coverage of the tolerance interval (the target minimum percentage of population in the interval) |
| P* | Maximum percentage of the population in interval |
| ε | the margin of error of the tolerance interval |
| α* | the margin of error probability for the tolerance interval |
| n | the number of observations in the sample |
- Odeh, R. E., Chou, Y.-M. and Owen, D.B. (1987). The precision for coverages and sample size requirements for normal tolerance intervals. Communications in Statistics: Simulation and Computation, 16, 969–985.
Calculating sample size and maximum acceptable percentages of population for interval for nonparametric tolerance intervals
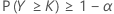
That is n – k = FW–1 (1 – α), where FW–1(.) represents the inverse cumulative distribution function of W = n – Y.
Similarly, it can be shown that a one-sided (1 – α, P) upper tolerance limit is given by X( n – k + 1 ), where k satisfies the above conditions for lower limit.
In both cases the actual or effective coverage is given as P(Y > k).
In addition, a two-sided (1 – α, P) tolerance interval may be given as (Xr, Xs) where k = s – r is the smallest integer that satisfies the following condition:
It has become common practice to take s = n – r + 1 so that r = ( n – k + 1) / 2. Both r and s are rounded down to the nearest integer. The actual or effective coverage is given by P( V ≤ k – 1).
Criterion
The criterion for sample size calculations for nonparametric tolerance intervals (both one-sided and two-sided) are similar to those described for normal data. More specifically, for a one-sided (1 – α, P) lower tolerance limit the criterion consists of determining the sample size, n, and the largest integer k that satisfy the following conditions:
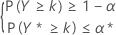
This condition is equivalent to finding n and the largest integer k that satisfy the following conditions:
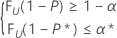
where FU(.) represents the cumulative distribution function of a random variable U which is distributed as a beta distribution with parameters α = k and b = n – k + 1.
As pointed out in Hahn and Meeker1 the criterion yields sample size requirements that are identical for both one-sided and two-sided tolerance intervals. Thus, we use the above criterion for both one-sided and two-sided intervals.
For given values of ε, P, and α*, Minitab uses an iterative algorithm to find the minimum sample size that satisfies the above two conditions. For given values of n, P, and α*, Minitab also calculates the margin of error that satisfies the above conditions using an iterative algorithm, and then calculates the interval for maximum percentage of population in interval using the following formula.
P* = P + ε
For additional details, see Hahn and Meeker1.
Notation
| Term | Description |
|---|---|
| 1 - α | the confidence level of the tolerance interval |
| P | the coverage of the tolerance interval (the target minimum percentage of population in the interval) |
| P* | Maximum percentage of the population in interval |
| ε | the margin of error of the tolerance interval |
| α* | the margin of error probability for the tolerance interval |
| n | the number of observations in the sample |
- Hahn, G. J. and Meeker, W. Q. (1991), Statistical Intervals: A Guide for Practitioners. John Wiley & Sons, 170.
